 |
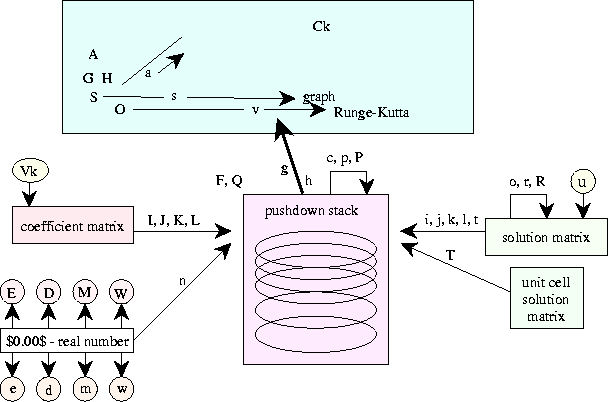
Having a specialized REC for solving differential equatioms, or more precisely, graphing their solutions, we need to survey its vocabulary. Fourth, or possibly sixth, order Runge-Kutta is the central process, advancing from one grid point to the next. Paralleling this movement, any of the elements of the coefficient matrix or of the solution matrix (or its trace, useful for stability arguments) can be made to follow along with cursor-moving operations. By maintaining horizons and providing for offsets, the graphing can be done with hidden line suppression, albeit in its most primitive form without exact intersections of the curves with their horizons.
REC-R assigns practically the whole alphabet to operators and predicates. However, they can be grouped into just a few categories, which can now be mentioned, although fuller descriptions will be given later on in another section. Basically, there is a very short pushdown list, which mostly holds the coordinates of a graph under construction.
Two graphing styles are available, both with possible hidden-line suppression. One represents elements of the Runge-Kutta matrices as functions of the independent variable, the other graphs some components as functions of others, as befits a phase plane. The choice depends on the selection of coordinates for the line drawer.
A variety of parameters can be defined by using the floating point number operator and then sending its value to a destination, which could even be the top of the pushdown stack.
Finally there are the Runge-Kutta integrators, the pen movements, and some predicates which can be used to vary pen parameters.