



Next: Subrutina PAGE
Up: Subrutinas que usa el
Previous: Subrutina INDO
Contents
La subrutina GRAF tiene varias funciones pero principalmente
sirve para graficar las coordenadas como funciones del tiempo.
Se escribe en una serie de hojas los valores de  ,
,  ,
,
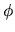 ; eso ocupa veinte columnas, en las cien restantes, se
imprime, bien, una estrella, un signo más o bien, un punto (o
posiblemente varios como veremos luego) en posiciones que indican
los valores que van tomando dichas variables.
La idea consiste simplemente en que una columna nos representa en
cifras los valores de tales variables, de tal manera que podemos
escribir los resultados hasta el número de cifras deseado aunque
muchas veces resulta dificil descifrar una columna de signos de
números. Sabemos que en cien columnas no hay mucha precisión
(existe bastante ruido) y puede haber un error hasta de 1%, lo
que impide que se tenga una buena resolución en las gráficas.
Entonces, conviene ajustar la escala, centrar el intervalo y
colocar un símbolo en la columna deseada. Para guardar un
símbolo en una palabra lo que hay que hacer es guardar
ahí el código de dicho símbolo (código
EBCDIC). La manera de pasar información entre la computadora y
el equipo periférico para este tipo de datos es por medio del
formato A, por ejemplo:
; eso ocupa veinte columnas, en las cien restantes, se
imprime, bien, una estrella, un signo más o bien, un punto (o
posiblemente varios como veremos luego) en posiciones que indican
los valores que van tomando dichas variables.
La idea consiste simplemente en que una columna nos representa en
cifras los valores de tales variables, de tal manera que podemos
escribir los resultados hasta el número de cifras deseado aunque
muchas veces resulta dificil descifrar una columna de signos de
números. Sabemos que en cien columnas no hay mucha precisión
(existe bastante ruido) y puede haber un error hasta de 1%, lo
que impide que se tenga una buena resolución en las gráficas.
Entonces, conviene ajustar la escala, centrar el intervalo y
colocar un símbolo en la columna deseada. Para guardar un
símbolo en una palabra lo que hay que hacer es guardar
ahí el código de dicho símbolo (código
EBCDIC). La manera de pasar información entre la computadora y
el equipo periférico para este tipo de datos es por medio del
formato A, por ejemplo:
READ (2,200) III
200 FORMAT (100 A1)
nos dice que vamos a leer cien números, uno en cada
elemento del arreglo III. Son esos números precisamente
los códigos de los símbolos o letras que deseamos guardar.
Aquí, lo único que nos interesa es saber que los números
tratados con formato A dan lugar a ciertos símbolos.
Eso es lo fundamental para colocar un símbolo en una
línea que deseamos imprimir.
Los argumentos de GRAF son (III, Y, N).
- III
- es la imagen de la línea que se va a conservar en el
programa principal.
- Y
- es el vector que contiene las coordenadas.
- N
- es un número que indica de que manera vamos a tratar la
línea; esta variable puede tomar valores de uno a cuatro, los
cuales explicaremos enseguida:
- N=1:
- Limpiamos la línea colocando la letra I en la
columna para representar el eje.
- N=2:
- Posiciona los simbolos: +, *, . de
acuerdo con el valor de
 ,
,  ,
, 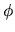 .
.
- N=3:
- Imprimimos la línea. Se procede en esta forma
porque es posible que haya que colocar varios valores de la
variable en una línea antes de imprimirla.
- N=4:
- Sirve para escribir una línea final y cambiar de página
retornando luego al programa.
Todas estas tareas son controladas mediante un GO TO computado
como puede verse en el listado. Esta subrutina es realmente una
colección de subrutinas en parte independientes y en parte en
común, independientemente por que realizan diferentes tareas y
regresan al programa sin afectar a las otras partes, en común porque
usan las mismas variables.
A continuación mostramos el listado de esta subrutina:
SUBROUTINE GRAF (III,Y,N)
DIMENSION III(100),X(6),Y(6)
COMMON T,DT,H,ALFA,IPR,IPO,G1,G2,Z1,Z2,GPL,GMI,EPP,EPM,XK,MO
COMMON IC,IT,IG,IP
EQUIVALENCE (XI,X(1)),(ETA,X(2)),(PHI,X(3))
C
CALL CPYV (X,Y)
GO TO (1,2,3,4),N
C
1 CONTINUE
DO 12 ID=1,100
12 III(ID)=1H
III(50)=1HI
C
RETURN
2 CONTINUE
IF(XI-10)30,30,31
30 IXI=IFIX(XI*10.)
GO TO 32
31 IXI=IFIX(XI)
IF (100-IXI) 17,32,32
17 IXI=100
III(10)=1HI
32 III(IXI)=1H+
IETA=IFIX(ETA*50.)+50
III(IETA)=1H*
IF(PHI-3.141592)34,34,33
33 PHI=PHI-6.283184
34 IF(PHI+3.141592)35,35,36
35 PHI=PHI+6.283184
36 IPHI=IFIX(PHI/.06283184)+50
III(IPHI)=1H.
CALL CPYV (Y,X)
RETURN
C
3 CONTINUE
WRITE(3,311)XI,ETA,PHI,III
311 FORMAT (1X,F6.3,2F7.3,100A1)
C
RETURN
4 CONTINUE
WRITE (3,301) H,ALFA
301 FORMAT (' FINAL H =',F10.3,', ALPHA =',F10.3)
WRITE(3,305)
305 FORMAT (1H1)
RETURN
END
Debe notarse que la tarea esencial de GRAF está controlada
por el valor N=2 y es esta parte la que merece más
discusión.
Existen cien columnas para graficar y hay que decidir (calcular)
en qué columna se va a imprimir un símbolo. Sabemos que
 es mayor que la unidad pero no existe ninguna restricción
sobre su cota superior; para
es mayor que la unidad pero no existe ninguna restricción
sobre su cota superior; para  se tiene:
se tiene:
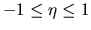 ,
, 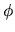 es una variable angular, entonces:
es una variable angular, entonces:
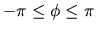 . Hay que reducir la variable a esos rangos; para
. Hay que reducir la variable a esos rangos; para  se
toma una convención que explicamos enseguida; en el intervalo
que mostramos en la figura va a representarse desde cero hasta
diez, como
se
toma una convención que explicamos enseguida; en el intervalo
que mostramos en la figura va a representarse desde cero hasta
diez, como  es mayor que la unidad nunca se usará para esta
variable el rango
es mayor que la unidad nunca se usará para esta
variable el rango 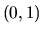 que viene representando por la parte
sombreada.
que viene representando por la parte
sombreada.
Figure 3.1:
rango de 
 |
Pero como es frecuente encontrar problemas donde
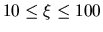 entonces se recurre a un truco: cuando eso
ocurre colocamos una letra I en la columna 10 y se usa una
escala que vaya hasta cien, eso es, se reduce por un factor de
diez la escala original. Si el valor de
entonces se recurre a un truco: cuando eso
ocurre colocamos una letra I en la columna 10 y se usa una
escala que vaya hasta cien, eso es, se reduce por un factor de
diez la escala original. Si el valor de  es mayor que cien,
se coloca únicamente un símbolo en el margen indicando que
se tiene un valor fuera de rango. Estas precauciones son
necesarias, porque si se tiene un índice que rebase los
límites del arreglo el dato es depositado en otra localidad
de las usadas por el programa, lo que causa serios problemas en
los resultados. Entonces, de acuerdo con lo convenido, si
es mayor que cien,
se coloca únicamente un símbolo en el margen indicando que
se tiene un valor fuera de rango. Estas precauciones son
necesarias, porque si se tiene un índice que rebase los
límites del arreglo el dato es depositado en otra localidad
de las usadas por el programa, lo que causa serios problemas en
los resultados. Entonces, de acuerdo con lo convenido, si
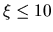 , usamos 0.1 por columna (son cien columnas), para
, usamos 0.1 por columna (son cien columnas), para
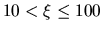 se toma 1.0 por columna, y para
se toma 1.0 por columna, y para 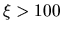 sólo
se coloca un símbolo en el margen.
La variable
sólo
se coloca un símbolo en el margen.
La variable  está comprendida entre
está comprendida entre 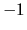 y
y 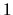 , entonces
tenemos un rango de
, entonces
tenemos un rango de 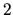 en cien columnas. Por lo tanto se tendrá
en cien columnas. Por lo tanto se tendrá
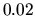 por columna; como
por columna; como  puede ser negativa hay que tomar
el cero de dicha variable hasta la columna cincuenta, haciéndose
por lo tanto 1 la conversión necesaria:
puede ser negativa hay que tomar
el cero de dicha variable hasta la columna cincuenta, haciéndose
por lo tanto 1 la conversión necesaria:
Para tratar a la variable 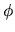 lo primero que debe hacerse es
checar si no es demasiado grande, si ese es el caso le restamos
lo primero que debe hacerse es
checar si no es demasiado grande, si ese es el caso le restamos
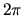 pues se supone que se ha iniciado en el rango
pues se supone que se ha iniciado en el rango
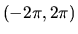 , graficamos con una frecuencia adecuada de modo que no pase
por
, graficamos con una frecuencia adecuada de modo que no pase
por 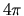 ó algo por el estilo. Igualmente hay que checar que
ó algo por el estilo. Igualmente hay que checar que
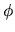 no sea demasiado negativa sumándole
no sea demasiado negativa sumándole 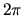 cuando ese
caso se presente. Esas operaciones mantienen a
cuando ese
caso se presente. Esas operaciones mantienen a 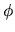 dentro de
su rango y al graficar se va a representar
dentro de
su rango y al graficar se va a representar
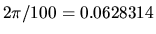 por columna. En la columna 50 pondremos el cero de dicha variable
y por lo tanto hay que darle el mismo tratamiento que se dio a
por columna. En la columna 50 pondremos el cero de dicha variable
y por lo tanto hay que darle el mismo tratamiento que se dio a
 . Debido a que ajustamos a
. Debido a que ajustamos a 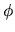 en este programa hay que
hacer también un reajuste en el programa principal porque debe
recordarse que estamos trabajando con una copia del vector y no
con el vector mismo por eso copiamos X en Y al
regresar el programa.
Los símbolos que se toman para
en este programa hay que
hacer también un reajuste en el programa principal porque debe
recordarse que estamos trabajando con una copia del vector y no
con el vector mismo por eso copiamos X en Y al
regresar el programa.
Los símbolos que se toman para  ,
,  , y
, y 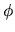 son: +,
* y . respectivamente y sus códigos son
son: +,
* y . respectivamente y sus códigos son 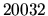 ,
,
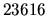 y
y 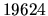 . En otras máquinas (3150 y PDP-10,
por ejemplo) se usa la instruccion:
. En otras máquinas (3150 y PDP-10,
por ejemplo) se usa la instruccion:
ARREGLO(J) = 1 H SIMBOLO
así lo usamos en algunos de nuestro listados.
Con esto ya sabemos como funciona una subrutina para graficar un
conjunto de variables su generalización a otros sistemas de
coordenadas es más o menos clara: hay que determinar el rango de
cada variable y garantizar que no se salga de dicho rango;
después, hay que buscar un factor adecuado para graficar dicha
variable en el intervalo disponible (en este caso es de uno a
cien). También podemos subdividir una subrutina de ese tipo
varias partes, por ejemplo, si queremos: preparar una línea
nueva, insertar un dato en una línea, imprimir una línea
etc. También podemos imprimir en el margen algunos datos
importantes, en fin hay muchas posiblilidades; pero la técnica
es esencialmente la que hemos descrito.
Otra cosa importante que debe señalarse es la razon de haber
separado la inserción de símbolos de la impresión de
datos: debido a la poca resolución que se tiene al graficar es a
veces conveniente (cuando hay variaciones muy rápidas) poner
más de un punto al imprimir una línea porque no se puede
saber precisamente cuál es la transición entre un punto y otro
en dos líneas contiguas, aunque no siempre se logra una
resolución completa (ver los ejemplos) pero las curvas se
suavizan un poco, siendo más faciles de entender. El número de
puntos lo indica la variable IPR com ya se dijo antes,
mientras que IPO es el número de líneas deseado.
Cuando hay variaciones rápidas es también conveniente reducir el
incremento de tiempo, cambiar intervalo de imprensión o cosas
por el estilo. Se ha convenido también en que cuando una curva
cruza el eje, la letra I que existe originalmente en esa
posicion es reemplazada por el símbolo que representa a la
curva. Ya sabemos como graficar; pero hay todavía muchas
cosas que discutir. Eso corresponde a otras subrutinas.




Next: Subrutina PAGE
Up: Subrutinas que usa el
Previous: Subrutina INDO
Contents
Pedro Hernandez
2006-02-20
 ,
,  ,
, 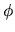 .
.