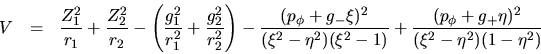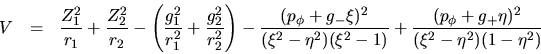Subrutina REGP

Esta subrutina es propiamente dos subrutinas fundidas en una sola, pero hemos preferido construirla así porque nos ahorra un poco de trabajo, una de sus tareas consiste en obtener una gráfica para ver cuál es la región donde puede moverse una partícula, según los valores que tengan los parámetros que definen su movimiento. La región permitida aparece en blanco; el área sombreada es prohibida. La manera de hacerlo es bastante simple (pero si no la explicamos no se entiende) y es la siguiente: Se calculan los valores de $\xi$ y de $\eta$ en cada punto y una vez hecho eso, calculamos el polinomio de cuarto grado que define al momento, eso para cada variable;

C   ***********************************************************************
C   *                                                                     *
C   *  LA SUBRUTINA "REGP" SIRVE PARA GRAFICAR LA REGION PERMITIDA Y LA   *
C   *  REGION PROHIBIDA EN EL PROBLEMA DE DOS CENTROS, ADEMAS PUEDE       *
C   *  CALCULAR LOS NIVELES DE ENERGIA POTENCIAL CONSTANTE                *
C   *                                                                     *
C   ***********************************************************************
     SUBROUTINE REGP (IX)
     COMMON AZ,BZ,X,IXIN,IETN,III(600),JJJ(600),H,ALFA,PFI,G1,G2,Z1,Z2,
    @ EPP,EPM,GMI,GPL,JII(120)
     DIMENSION IJK(120)
     DO 10 I=1,50
     DO  1 J=1,120
  1  IJK(J)=1H
     Y=(50-I)*0.08333
     DO 11 J=1,120
     Z=J*0.05-3.
     S1=(Z+1.0)**2+Y*Y
     S2=(Z-1.0)**2+Y*Y
     R1=SQRT (S1)
     R2=SQRT (S2)
     XI=(R1+R2)/2.
     ETA=(R1-R2)/2.
     GO TO (20,30) ,IX
  20 CONTINUE
     IXIN=0
     IETN=0
     CALL POLN (1,XI,H,-EPP,-(GMI,*GMI/2.+H+ALFA),EPP-2.*PFI*GMI,GMI*GMI
    @/2.-ALFA-PFI2)
     CALL POLN (2,ETA,H,EPM,-(H+ALFA+GPL*GPL/2.),-(EPM+2.*PFI*GPL),ALFA
    @-PFI2-GPL*GPL/2.)
     IF ((IXIN.NE.1) .AND. (IETN.NE.1)) GO TO 4
     IJK(J)=1H-
     GO TO 5
   4 IJK(J)=1H
   5 IJK (40)=1H:
     IJK (60)=1HI
     IJK (80)=1H:
     GO TO 11
  30 CONTINUE
     XI2=XI*XI
     ETA2=ETA*ETA
     XXI=XI2-1.
     EETA=1.-ETA2
     D=XI2-ETA2
     C1=(2.*PFI*GMI*XI+GMI*GMI*XI2)/(D*XXI)
     C2=(2.*PFI*GPL*ETA+GPL*GPL*ETA2)/(D*EETA)
     C3=PFI*PFI/(D*XXI)
     C4=PFI*PFI/(D*EETA)
     V1=Z1*Z1/R1+Z2*Z2/R2-G1*G1/S1-G2*G2/S2
     U=V1+C1+C2+C3+C4
     U=10.*U
     IF (U-10.) 21,21,43
  21 IF (U+10.) 41,22,22
  22 IF (U)     29,29,33
  29 IF (U+0.5) 31,31,41
  31 IF (U+1.)  32,32,11
  32 U=U+1.
     GO TO 29
  33 IF (U-0.5) 11,11,34
  34 IF (U-1.)  43,43,35
  35 U=U-1.
     GO TO 33
  41 IJK(J)=1H-
     GO TO 11
  43 IJK(J)=1H+
     IF (ABS(U).LT.0.07) IJK(J)=1H*
  11 CONTINUE
     WRITE (3,320) IJK
 320 FORMAT (1X,120A1)
  10 CONTINUE
     IF (IX.GT.1) GO TO 73
     WRITE (3,350)
 350 FORMAT   (/,20X,' LA REGION PROHIBIDA ES LA SOMBREADA, LA PARTICULA
    @  PUEDE MOVERSE EN LA PARTE EN BLANCO')
 73  CONTINUE
     WRITE (3,321)
 321 FORMAT (1H1)
     RETURN

después preguntamos por el signo del polinomio, eso lo decide el valor de los indicadores IXIN e IETA; cuando simultáneamente ambos son diferentes de la unidad, eso significa que la raíz del polinomio no resulta imaginaria y los momentos son reales, por lo tanto, en ese punto va a quedar un espacio en blanco; si alguno de los indicadores tiene el valor 1 su respectivo momento es imaginario y quedamos en que los dos momentos deben ser reales, siendo así ponemos en esa posición el símbolo menos (-) o tal vez otro que nos gusta más. Este proceso se repite para todos los puntos. Cuando se termina de imprimir la gráfica, se escribe un texto al pie de página (vea las gráficas) y regresa al programa. La otra tarea que puede realizar la subrutina que estamos discutiendo es la de obtener una gráfica semejante a las que se realiza con CNTU del programa TWOC. El potencial que se usa en este programa es:

$$\begin{eqnarray*} V & = & \frac{Z_1^2}{r_1} + \frac{Z_2^2}{r_2} - \left(\fra... ...} + \frac{(p_\phi + g_+\eta)^2}{(\xi^2 - \eta^2)(1 - \eta^2)} \end{eqnarray*}$$

Cuando no hay cargas eléctricas debemos tener el potencial equivalente al usado por Störmer [5] en el caso de las particulas en el campo magnético terrestre, aunque la expresión no sea la misma por el camino que hemos seguido nosotros. El criterio para formar los contornos de energía potencial constante lo vimos ya al discutir la subrutina CNTU y TWOC y no lo volveremos a discutir aquí. La subrutina REGP tiene solamente un argumento (IX) que es el que indica el tipo de tarea deseada, ese truco lo hemos usado ya muchas veces y como es sabido, el control se realiza mediante un GO TO computado y con eso queda explicado el papel de nuestra subrutina.