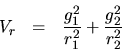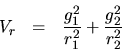Next: Interpretación de algunos resultados
Up: F A C U
Previous: Programa principal
Contents
Hemos dicho ya muchas veces que para poder separar la hamiltoniana
se le suma un potencial repulsivo y ese ha sido el tema de casi
todo lo que hemos hecho a lo largo de nuestro trabajo; pero como
las ecuaciones diferenciales que resultan por el hecho de omitir
dicho potencial no afectan el método de integración, podemos
usar todavía el programa TWOC modificandolo, alternando
las subrutinas que no sean convenientes y omitiendo las que no den
ya ninguna información; viendo todo con calma, sólo hay que
modificar la subrutina GRAD y hacer ajustes en el programa
principal; podemos alterar CNTU lo que no tiene caso porque
en REGP del programa PRYPO consideramos ya esos
cambios; al fin de cuentas, nos importa ver cómo son las
trayectorias y cómo resultan las curvas para las coordenadas en
función del tiempo. No tenemos interés en los resultados de
TURN porque los cálculos que realiza dependen de la
separación, tampoco nos interesa la constante 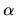 por las
mismas razones. Por fin de cuentas sólo hay que alterar la
subrutina GRAD sumando al hamiltoniano el término
por las
mismas razones. Por fin de cuentas sólo hay que alterar la
subrutina GRAD sumando al hamiltoniano el término
hay que modificar también las expresiones para las derivadas de los
momentos (las derivadas de las coordenadas no se alteran) agregando las
derivadas parciales con respecto a  o
o  según sea el caso.
según sea el caso.
SUBROUTINE GRAD (Y,DY)
DIMENSION X(6),DX(6),Y(6),DY(6)
COMMON T,DT,H,ALFA,IPR,IPO,G1,G2,Z1,Z2,GPL,GMI,EPP,EPM,XK,MO
COMMON IC,IT,IG,IP
EQUIVALENCE (XI,X((1)),(ETA,X(2)),(PHI,X(3))
EQUIVALENCE (PXI,X(4)),(PETA,X(5)),(PPHI,X(6))
EQUIVALENCE (DXI,DX(1)),(DETA,DX(2)),(DPHI,DX(3))
EQUIVALENCE (DPXI,DX(4)),(DPETA,DX(5)),(DPPHI,DX(6))
C
CALL CPYV (X, Y)
D=XI*XI-ETA*ETA
XXI=XI*XI-1.
EETA=1.-ETA*ETA
R1=XI+ETA
R2=XI-ETA
R12=R1*R1
R22=R2*R2
G12=G1*G1
G22=G2*G2
VR=-(G12/R12+G22/R22)
S1=G12/(R12*R12)
S2=G22/(R22*R22)
PPHX=(PPHI+GMI*XI)/XXI
PPHE=(PPHI+GPL*ETA)/EETA
HX=PXI*PXI+PPHX*PPHX
HE=PETA*PETA+PPHE*PPHE
U=(XXI*HX+EETA*HE+EPP*XI-EPM*ETA+XK)/D
H=U+VR
ALFA=XI*XI*U-XXI*HX-EPP*XI
DXI=PHI*XXI/D
DETA=PETA*EETA/D
DPHI=(PPHX*PPHE)/D
DEXI=(XI*U-XI*PXI*PXI-PPHX*(GMI-PPHX*XI)-EPP/2.)/D
DEETA=(ETA*PETA*PETA-PPHE*(GPL+PPHE*ETA)+EPM/2.-ETA*U)/D
DVRXI=S1+S2
DVERT=S1-S2
DPXI=DEXI+DVRXI
DPETA=DEETA+DVRET
DPPHI=0.0
C
CALL CPYV (DY,DX)
RETURN
END
Para no reescribir totalmente la subrutina es necesario hacer
algunas definiciones y reajustar las expresiones que aquí se
usan. Si recordamos que las expresiones para  y
y 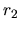 son
respectivamente
son
respectivamente 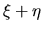 y
y 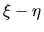 , podemos entonces
obtener las derivadas parciales de
, podemos entonces
obtener las derivadas parciales de 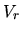 , con respecto a
, con respecto a  y a
y a
 y resultan muy simples. No hay mucho que discutir sobre
estos cambios si hemos seguido los pasos que nos traen hasta
aquí y no discutiremos más.
Hay que observar que de ninguna manera se va a alterar el proceso
de in tegración de Runge-Kutta, por lo que RUKU no se
enterará y seguirá funcionando como si nada ocurriera.
Otra cosa que esperamos ver es que las trayectorias de las
partículas van a presentar efectos de rizamiento y lo que creemos
es que aparecerán muchas pequeñas vueltas. Cuando haya solamente
cargas magnéticas debemos tener resultados semejantes a los de
Störmer.
En el programa principal solamente hay que hace pequeños cambios,
tales como excluir los llamados a ciertas subrutinas, escribir algunos
textos o hacer un ciclo para variar alguna de las cargas y observar el
efecto de dicha variación sobre las trayectorias.
Pueden hacerse otras modificaciones a TWOC, tales como
cambiar la subrutina RUKU y ver las diferencias en los
resultados segun varios de los métodos: no vamos a ver aquí
esos cambios, para ese efecto puede consultarse el trabajo de
Manuel González [21]. Con esto terminamos la discusión
de nuestro trabajo.
y resultan muy simples. No hay mucho que discutir sobre
estos cambios si hemos seguido los pasos que nos traen hasta
aquí y no discutiremos más.
Hay que observar que de ninguna manera se va a alterar el proceso
de in tegración de Runge-Kutta, por lo que RUKU no se
enterará y seguirá funcionando como si nada ocurriera.
Otra cosa que esperamos ver es que las trayectorias de las
partículas van a presentar efectos de rizamiento y lo que creemos
es que aparecerán muchas pequeñas vueltas. Cuando haya solamente
cargas magnéticas debemos tener resultados semejantes a los de
Störmer.
En el programa principal solamente hay que hace pequeños cambios,
tales como excluir los llamados a ciertas subrutinas, escribir algunos
textos o hacer un ciclo para variar alguna de las cargas y observar el
efecto de dicha variación sobre las trayectorias.
Pueden hacerse otras modificaciones a TWOC, tales como
cambiar la subrutina RUKU y ver las diferencias en los
resultados segun varios de los métodos: no vamos a ver aquí
esos cambios, para ese efecto puede consultarse el trabajo de
Manuel González [21]. Con esto terminamos la discusión
de nuestro trabajo.




Next: Interpretación de algunos resultados
Up: F A C U
Previous: Programa principal
Contents
Pedro Hernandez
2006-02-20