|
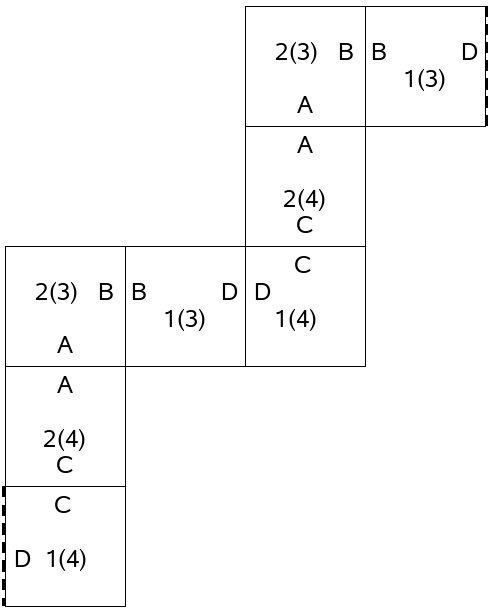
El flexágono cuadrado simple de ciclo irregular es usado para ilustrar la complejidad de el comportamiento dinámico de los flexágonos y para demostrar como un mapa completo (Fig 6) puede ser usado para interpretar y describir este comportamiento.
Así el flexágono armado está en la posición principal mostrada como en el diagrama izquierdo en la Fig 6. Las caras numeradas 2 y 1 son visible y estan en la posición principal 2(1). El primer número en el código esta identificando a una posición principal y esta indicando que el número visible en la superficie de la cara es el número 2 y el segundo número encerrado entre paréntesis, es visible en la cara de abajo y este corresponde al número 1. Si el flexágono fue cambiado de cara, tal que la cara numerada con el 1 fue primero entonces el código podría ser 1(2). Esto algunas veces no es necesariamente para indicar cual cara de el flexágono es primero. Las posiciones principales son planas y tienen doble rotación simétrica cercana a un eje vertical o 'Sectores'. Hay 2 pats adyacentes en un sector. En general en una posición principal de un flexágono tiene ![]() pats y
pats y ![]() sectores.
sectores.
Las líneas A-A y D-D en el diagrama superior izquierdo identifica las bisagras en el flexágono cuadrado, como es marcado en la red, y por lo tanto su orientación. Rotando a una posición principal del flexágono cuadrado por 180 grados cerca del eje vertical no lo hace diferente porque éste tiene doble rotación simétrica.
La orientación mostrada en la figura 6 son arbitrarias, y estas son elegidas para ayudar a la visualización del comportamiento dinámico del flexágono. En un flexágono cuadrado la posición principal tiene 2 grados de libertad en que la rotación puede ocurrir cerca de 2 diferentes líneas de la bisagra.
El mapa completo muestra que sucede cuando el flexágono cuadrado es doblado alrededor de su ciclo usando la técnica "sujetar y doblar". La descripción de abajo es para cruzar en la dirección de las flechas en la fig 6. Comenzando en la posición principal 2(1), doblando el flexágono cuadrado en 2, la línea a lo largo de la bisagra D-D para alcanzar la posición intermedia 2[4]. Manteniendo la bisagra de la línea superior y asegurando que las hojas numeradas con el 1 sean ocultadas. Una posición intermedia tiene la apariencia de 2 cuadrados, unidos en un lado común. Este tiene doble rotación simétrica cerca de la bisagra central, por ejemplo la bisagra de la línea A-A en la posición intermedia 2[4]. El diagrama superior del centro en la figura muestra la apariencia para un lado. Sólo un número es visible y este número es el primer número mostrado en el código. Abriendo el flexágono en la parte superior y revelando cerca de las bisagras B así como para alcanzar la posición principal 3(2). Continue doblando en orden cíclico para recorrer el periodo completo. Si el flexágono es cambiado, el ciclo puede ser recorrido en la dirección inversa.
En una posición principal esto es posible, para doblar un flexágono cuadrado en 2 ó 4 diferentes maneras para lograr cuatro diferentes posiciones intermedias. Mientras que para el flexágono cuadrado de ciclo simple irregular 2 de estas no conducen a otra posición principal. Tal posición intermedia no es normalmente mostrada en un mapa completo.