


Next: Tipo 1 o sensibles
Up: Jerarquía de Chomsky
Previous: Jerarquía de Chomsky
Contents
Este tipo de gramáticas son de la forma
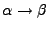 donde
donde
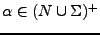 y
y
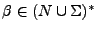 . Estas generan lenguajes recursivamente enumerables, que son aceptados por las máquinas de Turing, que es un autómata que lee y escribe en una cinta infinita. Hay dos tipos principales de máquinas de Turing, las determinístas y las no determinístas, la diferencia entre ellas es, que la determinísta, solo puede pasar a una configuración siguiente dados un estado actual y una entrada en la cinta, por otro lado, la no determinísta tiene un conjunto finito de configuraciones siguientes a las que puede llegar a partir de una estado actual y una entrada en la cinta. En un movimiento la máquina puede leer, escribir, y desplazarse en hacia la derecha o la izquierda de la cinta. La máquina de Turing parará siempre que llegue a un estado final. La secuencia de movimientos que conducen a una configuración de parada recibe el nombre de computación.
. Estas generan lenguajes recursivamente enumerables, que son aceptados por las máquinas de Turing, que es un autómata que lee y escribe en una cinta infinita. Hay dos tipos principales de máquinas de Turing, las determinístas y las no determinístas, la diferencia entre ellas es, que la determinísta, solo puede pasar a una configuración siguiente dados un estado actual y una entrada en la cinta, por otro lado, la no determinísta tiene un conjunto finito de configuraciones siguientes a las que puede llegar a partir de una estado actual y una entrada en la cinta. En un movimiento la máquina puede leer, escribir, y desplazarse en hacia la derecha o la izquierda de la cinta. La máquina de Turing parará siempre que llegue a un estado final. La secuencia de movimientos que conducen a una configuración de parada recibe el nombre de computación.
Existen algunas variaciones de este tipo de máquina. Aunque ninguna tiene más potencia para realizar una computación que la máquina de Turing original, hay casos en los que resulta más conveniente y cómodo utilizar algúna de sus variantes. Cualquiera de sus variantes puede ser emulada por la máquina original.



Next: Tipo 1 o sensibles
Up: Jerarquía de Chomsky
Previous: Jerarquía de Chomsky
Contents
Pablo Gerardo Padilla Beltran
2005-10-21