


Next: Expresiones Regulares
Up: Alfabetos y lenguajes
Previous: Operaciones con cadenas
Contents
El concepto de concatenación se puede extender a los lenguajes. Se define la concatenación de lenguajes como sigue:
El lenguaje que resulta de la concatenación de  y
y 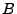 esta formado por la concatenación de todas la cadenas de
esta formado por la concatenación de todas la cadenas de  con todas la cadenas de
con todas la cadenas de 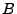 .
.
Ejemplo: Si
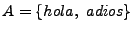 y
y
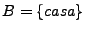 , entonces,
, entonces,
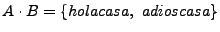 .
.
La concatenación de lenguajes se puede realizar aún si los lenguajes no estan contruídos sobre el mismo alfabeto, en tal caso la concatenación nos lleva a que, si  y
y 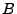 , son lenguajes sobre
, son lenguajes sobre 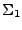 y
y 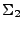 , entonces el lenguaje resultante será un lenguaje sobre
, entonces el lenguaje resultante será un lenguaje sobre
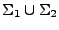 .
.
La cadena vacía se comporta como la identidad en cuanto a la concatenación de lenguajes se trata, ya que si tenemos
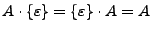 .
.
La definición de potencia, también puede extenderse a los lenguajes de la misma manera
Por lo tanto, si 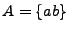 sobre un algún alfabeto, se tiene que
Hay que destacar que de la anterior definición se tiene que
sobre un algún alfabeto, se tiene que
Hay que destacar que de la anterior definición se tiene que
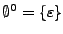 .
.
Dado que los lenguajes son conjuntos de cadenas, las operaciones, intersección, unión y sublenguaje se difinen como sigue:
Sean  y
y 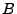 lenguajes sobre el alfabeto
lenguajes sobre el alfabeto  , la unión se denota como
, la unión se denota como 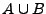 y quiere decir que el lenguaje resultante esta formado por todas la palabras que se encuentren en al menos uno de los dos lenguajes, más generalmente:
y quiere decir que el lenguaje resultante esta formado por todas la palabras que se encuentren en al menos uno de los dos lenguajes, más generalmente:
La intersección de los lenguajes  y
y 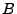 es un lenguaje formado por todas las cadenas que se encuentran tanto en
es un lenguaje formado por todas las cadenas que se encuentran tanto en  como en
como en 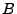 , esto es:
Con un ejemplo se prodrá ilustrar mejor las dos definiciones anteriores.
, esto es:
Con un ejemplo se prodrá ilustrar mejor las dos definiciones anteriores.
Ejemplo: Sean
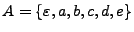 y
y
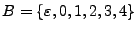 ,
Ahora hay que definir el concepto de sublenguaje, recordando la teoría de conjuntos sabemos que un conjunto
,
Ahora hay que definir el concepto de sublenguaje, recordando la teoría de conjuntos sabemos que un conjunto 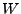 es un subconjunto de
es un subconjunto de 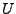 , si
, si 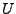 contiene a todos los elementos de
contiene a todos los elementos de 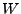 y se denota como
y se denota como
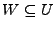 , y se lee, W es un subconjunto de U. Esta definición se puede mudar perfectamente a la teoría de lenguajes, diciendo que si
, y se lee, W es un subconjunto de U. Esta definición se puede mudar perfectamente a la teoría de lenguajes, diciendo que si  y
y 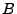 son lenguajes, entonces
son lenguajes, entonces 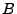 es un sublenguaje de
es un sublenguaje de  , si
, si  contiene todas las cadenas de
contiene todas las cadenas de 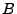 y se denota
y se denota
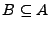 , y se lee B es un sublenguaje de A.
, y se lee B es un sublenguaje de A.
Sea 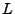 cualquier lenguaje sobre
cualquier lenguaje sobre  , entonces
, entonces
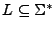 , ya que
, ya que 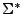 contiene todas las cadenas que son posibles de generar con el alfabeto
contiene todas las cadenas que son posibles de generar con el alfabeto  .
.
La igualdad de lenguajes cumple con las mismas caracteríscas que la igualdad entre conjuntos, sean  y
y 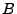 lenguajes, son iguales, sólo si, contienen exactamente las mismas cadenas. También hereda sus propiedades de la teoría de conjuntos, tales como son los siguientes teoremas:
lenguajes, son iguales, sólo si, contienen exactamente las mismas cadenas. También hereda sus propiedades de la teoría de conjuntos, tales como son los siguientes teoremas:
El teorema 2.3.1 sirve para demostrar la igualdad entre lenguajes y se utiliza para demostrar que la concatenación es distributiva con respecto a la unión de lenguajes.
Demostración.Supongamos que 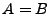 , entónces tenemos que probar que
, entónces tenemos que probar que
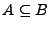 y
y
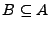 , para ello digamos que
, para ello digamos que 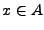 . Como
. Como 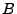 contiene las mismas cadenas que
contiene las mismas cadenas que  , diremos que
, diremos que 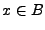 , de lo que se deduce que
, de lo que se deduce que
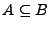 . De la misma forma, si
. De la misma forma, si 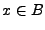 , entónces
, entónces 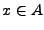 ya que los dos contienen las mismas cadenas, de lo anterior tenemos que
ya que los dos contienen las mismas cadenas, de lo anterior tenemos que
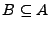 , lo cual no lleva a que
, lo cual no lleva a que
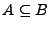 y
y
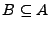 . Esto significa que las cadenas que estan en
. Esto significa que las cadenas que estan en 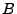 , están también en
, están también en  y viceversa, por lo que
y viceversa, por lo que 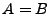 , con lo que se demuestra la igualdad.
, con lo que se demuestra la igualdad. 
Teorema 2.3.2
Dados los lenguajes 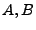 y
y 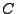 , sobre un alfabeto
, sobre un alfabeto  , se cumple que:
, se cumple que:
-
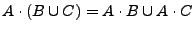
-
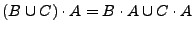
Demostración.Para demostrar la primera parte del teorema, probaremos primero que
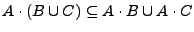 . Supongamos que
. Supongamos que
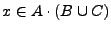 , y que
, y que
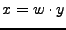 , donde
, donde 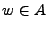 y
y
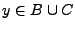 . Sí
. Sí 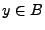 , tenemos que
, tenemos que
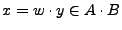 y por lo tanto
y por lo tanto
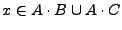 . Si
. Si 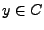 , tenemos que
, tenemos que
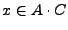 y de nuevo
y de nuevo
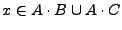 . Sin importar a que lenguaje pertenesca
. Sin importar a que lenguaje pertenesca 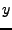 , se deduce que
, se deduce que
Ahora para probar
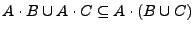 suponemos que
suponemos que
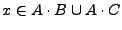 de modo que
de modo que
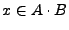 o
o
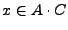 . Si
. Si
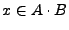 y
y
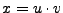 donde
donde 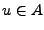 y
y 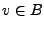 , tenemos que
, tenemos que
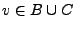 , y ya que
, y ya que 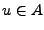 , tenemos que
, tenemos que
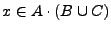 . Por otro lado si
. Por otro lado si
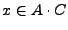 y si
y si
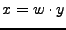 , tenemos que
, tenemos que 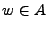 y
y 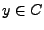 , por lo tanto
, por lo tanto
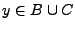 y ya que
y ya que 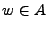 , tenemos que
, tenemos que
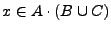 . De lo anterior se deduce que
. De lo anterior se deduce que
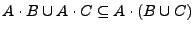 . Utilizando el teorema 2.3.1 se obtiene que
. Utilizando el teorema 2.3.1 se obtiene que
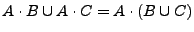 , lo que demuestra la igualdad.
, lo que demuestra la igualdad. 
De forma muy similar se demuestra la segunda parte del teorema 2.3.2. Así que no aparecerá la demostración en este documento.
A diferencia de la unión, la concatenación no es distributiva con respecto a la intersección de lenguajes, para esto, hay que proponer que, si
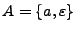 ,
,
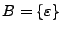 y
y 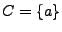 , entoces
, entoces
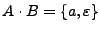 y
y
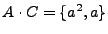 , por lo que
, por lo que
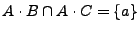 . Pero tenemos que
. Pero tenemos que
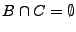 , entonces
, entonces
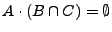 , por lo tanto:
, por lo tanto:
Ahora veremos dos conceptos más, el primero es el de cerradura de Kleene o cerradura estrella, élla esta definida como la unión de 0 o más potencias de un lenguaje  sobre un alfabeto
sobre un alfabeto  , más precisamente, la cerradura de Kleene es realizar 0 o más concatenaciones del lenguaje
, más precisamente, la cerradura de Kleene es realizar 0 o más concatenaciones del lenguaje  con él mismo, y se denota
con él mismo, y se denota
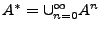 ,
lo que resulta en un lenguaje que contiene todas las cadenas que son posibles de formar sobre
,
lo que resulta en un lenguaje que contiene todas las cadenas que son posibles de formar sobre  . También tenemos a la cerradura positiva, que es la unión de una o más potencias de
. También tenemos a la cerradura positiva, que es la unión de una o más potencias de  en
en  , resultando en un lenguaje que contiene, todas las cadenas excepto la cadena vacía
, resultando en un lenguaje que contiene, todas las cadenas excepto la cadena vacía
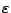 , y se denota
, y se denota
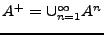 .
.
Un factor importante que debe recordarse es que la diferencia entre estos dos tipos de cerradura es, que en la cerradura de Kleene se realiza con 0 o más concatenaciones, en cambio la cerraduta positiva se realiza con 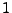 o más concatenaciones.
o más concatenaciones.
Ejemplo: Si  es el alfabeto español y
es el alfabeto español y 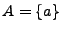 sobre
sobre  , tendremos que
, tendremos que
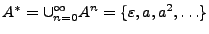 , ya que
, ya que
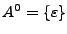 y
y
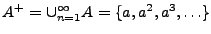 .
.
La definición de la cerradura de Kleene es igual a la de el lenguaje universal, mencionada en la sección 2.4 en la página ![[*]](crossref.png) . Sea
. Sea  un alfabeto,
un alfabeto,
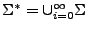 es la concatenación de 0 o más símbolos de
es la concatenación de 0 o más símbolos de  , que son las cadenas que conforman el lenguaje universal que también se denota
, que son las cadenas que conforman el lenguaje universal que también se denota 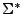 , de aquí que todo lenguaje sobre
, de aquí que todo lenguaje sobre  es un sublenguaje de
es un sublenguaje de 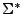 .
.
La diferencia entre lenguajes sigue las mismas reglas que para la diferencia en conjuntos, es decir, si  y
y 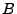 son lenguajes sobre
son lenguajes sobre  , entonces
, entonces
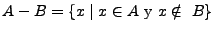 , que resulta en un lenguaje que contiene todas las cadenas de
, que resulta en un lenguaje que contiene todas las cadenas de  , que no estan en
, que no estan en 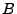 .
.
Al igual que con conjutos se puede definir el complento de un lenguaje. Sea  un lenguaje sobre
un lenguaje sobre  su complemento es
su complemento es
se puede que ver la definición se plantea de la misma manera que con conjuntos, donde el lenguaje complemento contiene todas las cadenas del lenguaje universal 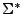 , que no estan en
, que no estan en  .
.
El inverso de un lenguaje se denota como 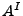 y su efecto sobre el lenguaje es que todas las cadenas del lenguaje se invierten, esto es, si
y su efecto sobre el lenguaje es que todas las cadenas del lenguaje se invierten, esto es, si  es un lenguaje, su inverso es
es un lenguaje, su inverso es
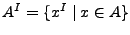 .
.
Ejemplo: Si
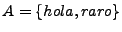 , entonces
, entonces
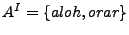 .
.
El inverso de un lenguaje se anula a sí mismo. Al igual que con las cadenas, el inverso del inverso de un lenguaje, deja el lenguaje original intacto, esto es, 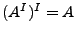 .
.
El uso de el inverso de un lenguaje es bueno para casí todas las operaciones sobre lenguajes, pero en el caso de la concatenación, no solo invierte las palabras concatenadas de los lenguajes, sino que también cambia el ordan de la concatenación de los lenguajes,
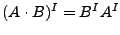 .
.



Next: Expresiones Regulares
Up: Alfabetos y lenguajes
Previous: Operaciones con cadenas
Contents
Pablo Gerardo Padilla Beltrán
2005-10-21
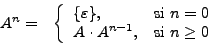
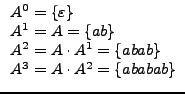
![]() y
y ![]() lenguajes sobre el alfabeto
lenguajes sobre el alfabeto ![]() , la unión se denota como
, la unión se denota como ![]() y quiere decir que el lenguaje resultante esta formado por todas la palabras que se encuentren en al menos uno de los dos lenguajes, más generalmente:
y quiere decir que el lenguaje resultante esta formado por todas la palabras que se encuentren en al menos uno de los dos lenguajes, más generalmente:
![]() , entónces tenemos que probar que
, entónces tenemos que probar que
![]() y
y
![]() , para ello digamos que
, para ello digamos que ![]() . Como
. Como ![]() contiene las mismas cadenas que
contiene las mismas cadenas que ![]() , diremos que
, diremos que ![]() , de lo que se deduce que
, de lo que se deduce que
![]() . De la misma forma, si
. De la misma forma, si ![]() , entónces
, entónces ![]() ya que los dos contienen las mismas cadenas, de lo anterior tenemos que
ya que los dos contienen las mismas cadenas, de lo anterior tenemos que
![]() , lo cual no lleva a que
, lo cual no lleva a que
![]() y
y
![]() . Esto significa que las cadenas que estan en
. Esto significa que las cadenas que estan en ![]() , están también en
, están también en ![]() y viceversa, por lo que
y viceversa, por lo que ![]() , con lo que se demuestra la igualdad.
, con lo que se demuestra la igualdad. ![]()
![]() . Supongamos que
. Supongamos que
![]() , y que
, y que
![]() , donde
, donde ![]() y
y
![]() . Sí
. Sí ![]() , tenemos que
, tenemos que
![]() y por lo tanto
y por lo tanto
![]() . Si
. Si ![]() , tenemos que
, tenemos que
![]() y de nuevo
y de nuevo
![]() . Sin importar a que lenguaje pertenesca
. Sin importar a que lenguaje pertenesca ![]() , se deduce que
, se deduce que
![]() ,
,
![]() y
y ![]() , entoces
, entoces
![]() y
y
![]() , por lo que
, por lo que
![]() . Pero tenemos que
. Pero tenemos que
![]() , entonces
, entonces
![]() , por lo tanto:
, por lo tanto:
![]() o más concatenaciones.
o más concatenaciones.
![]() es el alfabeto español y
es el alfabeto español y ![]() sobre
sobre ![]() , tendremos que
, tendremos que
![]() , ya que
, ya que
![]() y
y
![]() .
.
![[*]](crossref.png) . Sea
. Sea ![]() un alfabeto,
un alfabeto,
![]() es la concatenación de 0 o más símbolos de
es la concatenación de 0 o más símbolos de ![]() , que son las cadenas que conforman el lenguaje universal que también se denota
, que son las cadenas que conforman el lenguaje universal que también se denota ![]() , de aquí que todo lenguaje sobre
, de aquí que todo lenguaje sobre ![]() es un sublenguaje de
es un sublenguaje de ![]() .
.
![]() y
y ![]() son lenguajes sobre
son lenguajes sobre ![]() , entonces
, entonces
![]() , que resulta en un lenguaje que contiene todas las cadenas de
, que resulta en un lenguaje que contiene todas las cadenas de ![]() , que no estan en
, que no estan en ![]() .
.
![]() un lenguaje sobre
un lenguaje sobre ![]() su complemento es
su complemento es
![]() , entonces
, entonces
![]() .
.
![]() .
.
![]() .
.