

Next: Clasificación de lenguajes
Up: Alfabetos y lenguajes
Previous: Expresiones Regulares
Contents
Autómata Finito
Recordando lo visto en la sección 2.4, una expresión regular es una forma de describir un lenguaje, pero, ¿Cómo haríamos para saber si una cadena pertenece o no al lenguaje?
Una forma de hacerlo es construyendo un diagrama que contenga la información necesaria para analizar la cadena, este diagrama tendrá forma de grafo dirigido1. La cadena será leída de izquierda a derecha.
Para dar a conocer que la cadena es aceptada, se debe establecer un estado de aceptación y también se deben establecer estados de no aceptación para terminar el análisis de las cadenas que no pertenescan al lenguaje. Los estados, tanto de aceptación como los que no lo son, serán representados por medio de nodos en el grafo, los cuales es conveniente etiquetar de alguna forma, así que definiremos
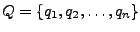 como el conjunto finito de todos los estados posibles,
como el conjunto finito de todos los estados posibles, 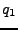 será el estado inicial y
será el estado inicial y
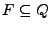 será el conjunto finito de todos los estados finales, es decir, estados de aceptación.
será el conjunto finito de todos los estados finales, es decir, estados de aceptación.
Tomaremos a la cadena que será analizada como nuestro alfabeto de entrada y lo denotaremos como  . Cada arista en el grafo es etiquetada con un símbolo de
. Cada arista en el grafo es etiquetada con un símbolo de  que indica una transición de algún estado a otro en el sentido marcado por la flecha en algúno de los extremos de cada arista. Al analizar un carácter es posible permanecer en el mismo estado después de la transición. Los estados de aceptación deben de distinguirse de los demás, por lo que serán encerrados en un círculo.
que indica una transición de algún estado a otro en el sentido marcado por la flecha en algúno de los extremos de cada arista. Al analizar un carácter es posible permanecer en el mismo estado después de la transición. Los estados de aceptación deben de distinguirse de los demás, por lo que serán encerrados en un círculo.
Analizar una cadena es recorrer los caminos del grafo; dependiendo del carácter que esta siendo análizado se elige un camino a recorrer. Cuando se acepta una cadena como miembro del lenguaje se llega a un estado de aceptación (encerrados en un círculo) por lo que, todos los caminos que lleven a un estado de aceptación construyen palabras pertenecientes a el lenguaje.
Ejemplo: Si tenemos, el alfabeto
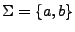 y el lenguaje descrito por la expresión regular
y el lenguaje descrito por la expresión regular
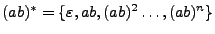 , para demostrar que la cadena
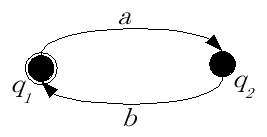
, para demostrar que la cadena 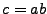 pertenece a este lenguaje construimos el diagrama de la figura 1.
pertenece a este lenguaje construimos el diagrama de la figura 1.
Figura 1:
Gráfo para analizar el lenguaje descrito por la expresión regular 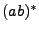
|
También se puede describir la forma en que la cadena es procesada por medio de un tabla, la cual contiene la información acerca de las transiciones que se realizan al recorrer la cadena. En dicha tabla tendremos relacionadas parejas de la forma
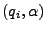 , donde
, donde 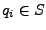 ,
,
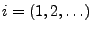 y
y 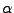 es un carácter de la cadena que se esta analizando. A partir de un estado y un carácter podremos decir cual será el camino que debe ser recorrido en el grafo, el cual nos llevará hacía algún estado en
es un carácter de la cadena que se esta analizando. A partir de un estado y un carácter podremos decir cual será el camino que debe ser recorrido en el grafo, el cual nos llevará hacía algún estado en 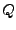 , por lo que podemos definir una función
, por lo que podemos definir una función
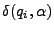 , que depende de dos variables, el estado actual y el carácter analizado, en otras palabras la función tomará pares de la forma
, que depende de dos variables, el estado actual y el carácter analizado, en otras palabras la función tomará pares de la forma
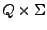 , para definir a que estado se llegará, entonces podemos definir más generalmene la función de transición de estados como sigue:
, para definir a que estado se llegará, entonces podemos definir más generalmene la función de transición de estados como sigue:
Sean 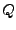 el conjunto de todos los estados,
el conjunto de todos los estados,  un alfabeto de entrada y
un alfabeto de entrada y 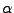 un carácter que pertenece a
un carácter que pertenece a  y
y 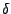 una función o regla de transformación, entonces
una función o regla de transformación, entonces 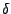 es de la forma
es de la forma
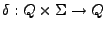 .
La tabla 1 describe como es analizada la cadena
.
La tabla 1 describe como es analizada la cadena 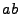 con el diagrama de la figura 1.
con el diagrama de la figura 1.
Tabla 1:
Tabla de transición de estados del diagrama de la figura 1.
|
|
Se puede apreciar que al analizar la cadena 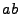 , primero se pasa de
, primero se pasa de 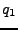 a
a 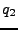 por medio de la arista
por medio de la arista 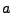 en el sentido indicado por la flecha, después cuando se analiza
en el sentido indicado por la flecha, después cuando se analiza 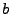 se pasa de
se pasa de 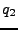 a
a 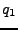 , por medio de la arista
, por medio de la arista 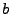 , la cadena a sido analizada por completo y
, la cadena a sido analizada por completo y 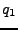 es un estado de aceptación, por lo que la cadena es aceptada como parte del lenguaje descrito por
es un estado de aceptación, por lo que la cadena es aceptada como parte del lenguaje descrito por 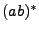 . Si tratamos de analizar otra cadena como
. Si tratamos de analizar otra cadena como 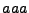 , podemos ver que no hay una transición definida para cuando uno está en el estado
, podemos ver que no hay una transición definida para cuando uno está en el estado 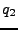 y se analiza una
y se analiza una 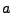 , por lo que se permanece en este estado. El cual no es un estado de aceptación y la cadena nunca termina de ser analizada, por lo que estamos seguros que
, por lo que se permanece en este estado. El cual no es un estado de aceptación y la cadena nunca termina de ser analizada, por lo que estamos seguros que 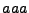 no pertenece a el lenguaje descrito por la expresión regular
no pertenece a el lenguaje descrito por la expresión regular 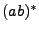 .
.
Supongamos que existe una máquina imaginaria que puede realizar la tarea de analizar cadenas y decir si éstas pertenecen a cierto lenguaje o no. Este tipo de máquinas son conocidas como máquinas de estados finitos o autómata finito(AF). El cual se define formalmente como una 5-tupla,
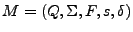 donde:
donde:
 , es algún alfabeto de entrada.
, es algún alfabeto de entrada.
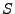 , es el conjunto finito de todos los estados.
, es el conjunto finito de todos los estados.
-
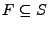 , es el conjunto de estados finales o de aceptación.
, es el conjunto de estados finales o de aceptación.
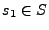 , es el estado inicial de la máquina(AF)
, es el estado inicial de la máquina(AF)
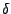 , es la función de transición de estados
, es la función de transición de estados
Existen varios tipo de autómatas, algunos de ellos serán brevemente descritos en la sección 2.6.2, indicando que tipo de lenguaje es capaz de reconocer cada uno. Así como hay diferentes tipos de autómata, existen diferentes tipos de lenguajes y cada uno de estos lenguajes pueden ser reconocidos por algún tipo de autómata.
Las diferencias entre los lenguajes radican en la forma en la que se estructuran, ésta estructura es definida por algún tipo de gramática, este concepto se analizará en la siguiente sección de una manera breve.



Next: Clasificación de lenguajes
Up: Alfabetos y lenguajes
Previous: Expresiones Regulares
Contents
Pablo Gerardo Padilla Beltrán
2005-10-21