Ejemplo 2

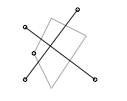
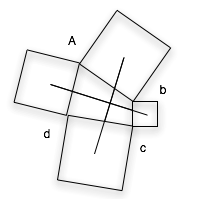
Si formamos un cuadrilátero con los lados de 4 cuadros como muestra la figura podemos demostrar que los dos vectores que se forman uniendo el centro de los cuadros que no son adyacentes son de igual magnitud y son perpendiculares.

Figura: Representación del ejemplo 2

Solución.- Tomaremos que los lados del cuadrilátero son vectores que al salir y llegar al mismo punto, suman cero $a+b+c+d = 0$. Si multiplicamos por dos está ecuación no se altera (para simplificar los cálculos). Ahora para obtener el centro del primer cuadrado marcado en la figura como $p$ recordemos que cualquier número complejo que multipliquemos por $i$ rota $\pi / 2$ y no altera su magnitud por lo que si sumamos $p = a + ia = a (1+i)$ nos dará el centro del cuadro. Para obtener los demás se hace algo similar y obtendremos las siguientes ecuaciones

$$q = 2a + b(1+i)$$

$$r = 2a+2b+c(1+i)$$

$$s = 2a+2b+2c+d(1+i)$$

Ahora definimos $a$ que es el vector que va desde $p$ a $r$ con $A = r-p$, de la misma manera a $B = s-q$. Substituyendo los valores nos quedará:

$$A = 2a+2b+2c+d(1+i)-(2a+b(1+i)) = b + 2c +d + i(d-b)$$

$$B = 2a+2b+c(1+i) - a (1+i) = a + 2b+c+i(c-a)$$

Ya que tenemos la definición de estos vectores en función de datos dados procedemos a demostrar que son de igual magnitud y perpendiculares. Para comprobar esto podemos hacer la ecuación $A+iB=0$ ya que si son perpendiculares y de igual magnitud se cumple que $A = iB$.

$$A+iB = b + 2c +d + i(d-b) + i(a + 2b+c+i(c-a))$$

$$= a+b+c+d+i(a+b+c+d) = 0 + i0= 0$$

En esta última ecuación recordemos las condiciones iniciales en las que $a+b+c+d = 0$

{($1,2$;)a  ($2,-1$;)b  ($-2,-3$;)c  ($-1,2$;)d
($20$Mp
(ZGp@aDgG@bD+gG@cD+gG@dD+g;)
(@aPY*+zS0p;)
(@aD@bPY*++zS1p;)
(@aD@bD+@cPY*++zS2p;)
(@aD@bD@cD++@dPY*++zS3p;)
(R2R0-R0QsG+g;)
(R3R1-R1QsG+g;)
;)}