Next: splitting quaternions
Up: Quaternions versus elementary matrices
Previous: Quaternions versus elementary matrices
The best way to get at 2x2 matrices, is to use quaternions. Starting from the natural basis for 2x2 matrices,
whose rule of multiplication is
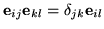 ,
quaternion-like matrices can be defined by
,
quaternion-like matrices can be defined by
In detail,
all built from sums and differences, thereby retaining real matrices. Like quaternions, these matrices anticommute (except for the identity). The ostensible difference is that only one square is 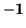 ,
the others are
,
the others are 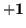 ,
changing Euler's formula from trigonometric to hyperbolic functions according to the sign.
,
changing Euler's formula from trigonometric to hyperbolic functions according to the sign.
The multiplication table is
The usual way of performing algebraic operations on these matrices is to write a sum such as
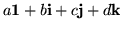 in the form
in the form
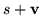 ,
where
,
where
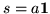 and
and 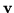 is the rest of the sum. One can adopt the custom of not writing an explicit
is the rest of the sum. One can adopt the custom of not writing an explicit 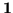 in places where the meaning is clear.
in places where the meaning is clear.
root
2000-03-17