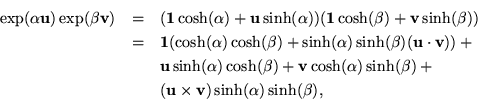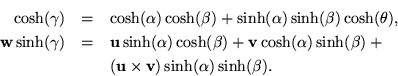Next: Visualizing products
Up: Lorentz Contraction
Previous: Square roots
An exponential is usually defined according to the traditional power series. Consider first the exponential of a vector:
 |
= |
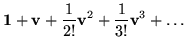 |
(60) |
| |
= |
![$\displaystyle [ {\bf 1}+ \frac{1}{2!}({\bf v}\cdot{\bf v}) + \frac{1}{4!}({\bf v}\cdot{\bf v})^2 + . . . ] +$](img211.gif) |
(61) |
| |
|
![$\displaystyle \frac{{\bf v}}{\surd({\bf v}\cdot{\bf v})} [\surd({\bf v}\cdot{\bf v})+\frac{1}{3!}\surd({\bf v}\cdot{\bf v})^3+\ldots ]$](img212.gif) |
(62) |
| |
= |
 |
(63) |
| |
= |
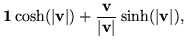 |
(64) |
a result analogous to Euler's formula. The exponential of a quaternion is not much more complicated, since any scalar which could be added would commute with the quaternion, so its exponential could just be set aside as a multiplying scalar factor. How much to set aside in the general case depends on satisfying the identity
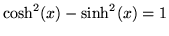 ,
but in general there is much to be said in favor of working with vectors of unit norm and treating norms separately.
,
but in general there is much to be said in favor of working with vectors of unit norm and treating norms separately.
Figure:
Arc length along the rectangular hyperbola defines hyperbolic trigonometry when the Lorentz metric is used.
|
The interesting properties of the exponential lie in its law of exponents. Notice that the angle,
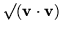 ,
is the norm of
,
is the norm of 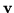 ,
and that imaginary quantities can be avoided by using trigonometric functions, such as should be done in association with the quaternion
,
and that imaginary quantities can be avoided by using trigonometric functions, such as should be done in association with the quaternion  .
.
Consider, for unit vectors 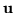 and
and 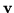 ,
,
and the prospects for seeing this as
Just define a new angle,
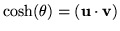 ;
then copy the two parts of the previous result:
;
then copy the two parts of the previous result:
Figure:
Quaternion exponentials and sequences of quaternion exponentials can be visualized in a nomogram based on the unit one-sheeted hyperboloid of radius squared -1.
 |




Next: Visualizing products
Up: Lorentz Contraction
Previous: Square roots
root
2000-03-17
![]() ,
is the norm of
,
is the norm of ![]() ,
and that imaginary quantities can be avoided by using trigonometric functions, such as should be done in association with the quaternion
,
and that imaginary quantities can be avoided by using trigonometric functions, such as should be done in association with the quaternion ![]() .
.
![]() and
and ![]() ,
,