Summary

In summary, although we may suspect that the last word has still not been said regarding symmetry and degeneracy in single-particle mechanics, we may still feel a satisfaction that some of its aspects at least are now understood. Although it has been primarily a quantum mechanical phenomenon, since degeneracy makes itself most visible in the multiplicity of degenerate energy levels, it turns out that its understanding is not uninteresting for classical mechanics either, one of the more noteworthy by-products of the understanding of the quantum mechanical realm having been the discovery of 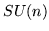$SU(n)$ as a universal symmetry group for classical mechanical systems. Needless to say, it is a disappointment that one could not have retained 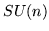$SU(n)$ as a quantum mechanical symmetry group as well, for it might then have been found to have some relation to the currently fashionable classification schemes for elementary particles. Even so it may still retain some utility in the limit of large quantum numbers, for which the effects of quantization wreak lesser havoc on the classical concepts.

The development of the theory of symmetry reflects in an interesting way the development of quantum mechanics and even present-day physics itself, presenting in a subtle way the suspicion that we do not really understand the workings of any physical process until we understand fully its symmetry properties. The history of the Dirac equation provides a nice illustration of this point. It has been a puzzle ever since its creation in 1928, although it immediately accounted for the electron spin and the experimental fine structure of the hydrogen atom. These were great successes, because the electron spin had previously been a purely ad hoc assumption, and the failure of the Klein-Gordon equation to give the hydrogen fine structure had left it in disrepute. However, the discovery of Zitterbewegung left a distinctly uneasy feeling about the mechanical interpretation of the movement of an electron, and the negative energy states which occurred in the solution required a definitive reformulation of quantum mechanical thinking, first with the introduction of the hypothesis of the electron sea and later with second quantization and the use of field theory. It was only after two decades, in 1950, that the Foldy-Wouthuysen transformation clarified the separation of positive and negative energy states, and set the Zitterbewegung in its proper perspective. It was at this same late date that the constant of the motion responsible for the residual twofold accidental degeneracy in the relativistic hydrogen atom was found by Johnson and Lippman.

Even then, it remained for the parity nonconservation experiments to show how incomplete the examination of the possible reflective symmetries of the Dirac equation had been, and another full decade before Biedenharn began to tamper with the Dirac Hamiltonian to produce a system with the degeneracy of the nonrelativistic hydrogen atom, and thus to begin to clarify the entanglement of relativistic effects with the spin-dependent, or more properly the multicomponent, aspects of the Dirac equation.

In the meantime, the Klein-Gordon equation has been rehabilitated and seen to apply to pi-mesonic atoms, relativistic wave equations have been written for systems with other intrinsic spins, and even the Dirac equation reformulated in alternative ways, including the two-component, second-order form introduced by Feynman and Gell-Mann.

To what should one attribute the degeneracy which occurs in many systems? Hidden symmetry is an attractive explanation, especially since the most generally known systems have had a very elegant interpretation in terms of hidden symmetry of one sort or another. However, it might seem that the existence of ladder operators and the separability of the equations of motion might be a sounder and more extensive basis from which to attempt the investigation of degeneracy. From the work of Infeld and Hull we know that ladder operators can be constructed for the most general sorts of second-order linear differential equations, of the type which habitually arises from quantum mechanical problems. Thus, separability seems to be the prevailing requirement, and ladder operators may be formed for separable systems even when there is no degeneracy at all. Degeneracy is then to be considered an exceptional circumstance depending upon the relative size of the steps taken by the various ladder operators. Moreover, even when there is degeneracy present, we have seen that it may not necessarily lead to the existence of either a small Lie group or to particularly interpretable transformations of phase space.

The foregoing remarks do not detract in any way from the beauty or elegance of the hidden symmetry concept in those situations where it applies, but they do limit the generality of such a concept as an interpretation of accidental degeneracy in every situation. In fact it is by no means clear at the present moment whether or not the classification of elementary particles will one day be fitted into a scheme resembling the harmonic oscillator or the bound states of the Kepler problem, wherein there will be not only symmetry operators but ladder operators running between different energy states, in such a way that the entire energy spectrum may be interrelated. Should such a systematic structure be found, it will no doubt rank with Mendeleev's table of the chemical elements or the scheme of nuclear magic numbers as a major triumph in our attempts to organize natural phenomena.

Acknowledgments

The manuscript has been completed during a period of leave spent at the Quantum Chemistry Department of Uppsala University, Sweden. It is a particular pleasure to thank M. en C. Roberto Mendiola, Director of the Escuela Superior de Física y Matemáticas, for his generosity in granting this period of leave, as well as to Prof. Per-Olov Löwdin for his excellent hospitality during this period. One cannot appreciate, without undertaking a project which requires extensive consultation of the literature, the value of the libraries which most research institutions have built up over the years, which makes it especially important to mention the role which UNESCO has played in helping secure similar facilities where such activities have only recently been initiated. This work could not have been begun without their assistance. Several students, Victor Dulock, Arturo Cisneros, Enrique Daltabuit, and Manuel Berrondo have, through their thesis work and in other ways, helped to resolve many of the aspects of single-particle symmetry and degeneracy which were not known whsn the article was begun, four years ago. Finally, I must record my appreciation of the patience which has been shown by the Editor, Dr. E. M. Loebl, while these investigations were made, and numerous personal and practical difficulties had to be surmounted.

REFERENCES

1.

H. V. McIntosh, On accidental degeneracy in classical and quantum mechanics. Amer. J. Phys. 27, 620-625 (1959).

2.

V. Fock, Zur Theorie des Wasserstoffatoms. Z. Physik 98, 145-154 (1935); see also V. A. Fock, Wasserstoffatom und nicht-euklidische Geometrie (mit einer Deutschen Zusammenfassung). Izv. Akad. Nauk USSR 2, 169-188 (1935).

3.

V. Bargmann, Zur Theorie des Wasserstoffatoms. Z. Physik 99, 576-582 (1936).

4.

W. Hamilton, On the application of the method of quaternions to some dynamical questions. Proc. Roy. Irish Acad. 3, 441-448 (1847); see also (Sir) W. R, Hamilton, ``Elements of Quaternions.'' Longmans, Green, New York, 1866.

5.

J. W. Gibbs and E. B. Wilson, ``Vector Analysis.'' Scribners and Sons, New York, 1901. Reprinted by Yale Univ. Press, New Haven, Connecticut, 1958.

6.

C. Runge, `` Vektoranalysis,'' English transl. Dutton, New York, 1919.

7.

W. Pauli, Jr., Über das Wasserstoffspektrum vorm Standpunkt der neuen Quantenmechanik. Z. Physik 36, 336-363 (1926).

8.

W. Lenz, Über den Bewegungsverlauf und die Quantenzustände der gestörten Keplerbewegung. Z. Physik 24, 197-207 (1924).

9.

B. L. van der Waerden, ``Sources of Quantum Mechanics,'' p. 58. North-Holland Publ., Amsterdam, 1967.

10.

L. Hulthén, Über die quantenmechanische Herleitung der Balmerterme. Z. Physik 86, 21-23 (1933).

11.

D. Podolsky and L. Pauling, The momentum distribution in hydrogenlike atoms, Phys. Rev. 34, 109-116 (1929).

12.

E. A. Hylleraas, Die Wellengleichung des Keplerproblems im Impulsraum Z. Physik 74, 216-224 (1932).

13.

O. Laporte and G. Y. Rainich, Stereographic parameters and pseudominimal hypersurfaces. Trans. Amer. Math. Soc. 39 154-182 (1936).

14.

O. Laporte, The connection between the Kepler problem and the four dimensional rotation group. Phys. Rev. 50, 400(A) (1936).

15.

J. M. Jauch, Groups of quantum mechanical contact transformations and the degeneracy of energy levels. Phys. Rev. 55, 1132(A) (1939).

16.

J. M. Jauch, On contact transformations and group theory in quantum mechanical problems. Ph.D. Thesis, Univ. of Minnesota, 1939.

17.

J. M. Jauch and E. L. Hill, On the problem of degeneracy in quantum mechanics. Phys. Rev. 57, 641-645 (1940).

18.

E. L. Hill, Seminar on the theory of quantum mechanics. Univ. of Minnesota, 1954 (unpublished).

19.

A. W. Saénz, On integrals of motion of the Runge type in classical and quantum mechanics. Ph.D. Thesis, Univ. of Michigan, 1949.

20.

G. A. Baker, Jr., Degeneracy of the 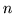$n$-dimensional isotropic, harmonic oscillator. Phys. Rev. 103, 1119-1120 (1956).

21.

V. A. Dulock, Jr., A study of accidental degeneracy in Hamiltonian mechanics. Ph.D. Thesis, Univ. of Florida, 1964; V. A. Dulock and H. V. McIntosh, On the degeneracy of the two-dimensional harmonic oscillator. Amer. J. Phys. 33, 109-118 (1965).

22.

Yu. N. Demkov, Group symmetry of an isotropic oscillator. Zh. Eksperim. Teor. Fiz. 26, 757 (1954); Symmetry group of the isotropic oscillator. Soviet Phys. JETP 9, 63-66 (1959); Bull. Leningrad State Univ. 11, 127 (1953); The definition of the symmetry group of a quantum system. The anisotropic oscillator. Soviet Phys. JETP 17, 1349-1351 (1963).

23.

L. A. Il'kaeva, Symmetry group of the anisotropic oscillator. Vestnik Leningrad. Univ. 22, 56-62 (1963) (in Russian).

24.

I. Vendramin, On the dynamical symmetry of the nonisotropic oscillators. Nuovo Cimento A bf 54, 190-192 (1968).

25a.

A. Cisneros, Estudio sobre el grupo universal de simetría. Professional Thesis, Polytech. Inst. of Mexico, 1968; A. Cisneros and H. V. McIntosh, Search for a universal symmetry group in two dimensions. J. Math. Phys. 11, 870-895 (1970).

25b.

G. Maiella and G. Vilasi, Reducible representations of the symmetry group of the anisotropic harmonic oscillator. Lett. Nuovo Cimento 1, 57-64 (1969).

26.

F. Klein and A. Sommerfeld, ``Theorie des Kreisels.'' Johnson Reprint Corp., New York, 1965.

27.

S. Epstein, Bermerkungen zur Frage der Quantelung des Kreisels. Physik. Z. 20, 289-294 (1919).

28.

F. Reiche, Zur Quantelung des asymmetrischen Kreisels. Physik. Z. 19, 394-399 (1918).

29.

H. A. Kramers. Über die Quantelung rotierender Moleküle. Z. Physik. 13, 343-350 (1923).

30.

H. A. Kramers and W. Pauli, Jr., Zur Theorie der Bandspektern. Z. Physik 13, 351-367 (1923).

31.

G. Kolossoff, Über Behandlung zyklischer Systeme mit Variationsprinzipien mit Anwendungen auf die Mechanik starrer Körper. Math. Ann. 60, 232-240 (1905).

32.

D. M. Dennison, The rotation of molecules. Phys. Rev. 23, 318-333 (1926).

33.

F. Reiche and Hans Rademacher, Die Quantelung des symmetrischen Kreisels nach Schrödingers Undulationsmechanik. Z. Physik 39, 444-464 (1926); H. Rademacher and F. Reiche, Die Quantelung des symmetrischen Kreisels nach Schrödingers Undulationsmechanik II. Z. Physik 41, 453-492 (1927).

34.

E. E. Witmer, The quantization of the rotational motion of the polyatomic molecule by the new wave mechanics. Proc. Nat. Acad. Sci. U.S.A. 13, 60-65 (1927).

35.

R. de L. Kronig, and I. I. Rabi, The symmetrical top in the undulatory mechanics. Phys. Rev. 29, 262-269 (1927).

36.

F. Lütgemeier, Zur Quantentheorie des drei- und mehratomigen Moleküls. Z. Physik 38, 251-263 (1926).

37.

F. Hund, Bemerkung über die Eigenfunktionen des Kugelkreisels in der Quantenmechanik. Z. Physik 51, 1-5 (1928).

38.

O. Klein, Zur Frage der Quantelung des symmetrischen Kreisels. Z. Physik 58, 730-734 (1929).

39.

H. A. Kramers and G. P. Ittman, Zur Quantelung des asymmetrischen Kreisels. Z. Physik 53, 553-565 (1929); Zur Quantelung der asymmetrischen Kreisels, II. Z. Physik 58, 217-231 (1929); Zur Quantelung der asymmetrischen Kreisels, III. Z. Physik 60, 663-681 (1930).

40.

S. C. Wang, On the asymmetric top in quantum mechanics. Phys. Rev. 34, 243-252 (1929).

41.

B. S. Ray, Über die Eigenwerte des asymmetrischen Kreisels, Z. Physik 78, 74-91 (1932).

42.

H. G. B. Casimir, Zur quantenmechanischen Behandlung des Kreiselproblems. Z. Physik 59, 623-634 (1930).

43.

G. W. King, R. M. Hainer, and P. C. Cross, The asymmetric rotor I: Calculation and symmetry classification of energy levels. J. Chem. Phys. 11, 27-42 (1943); P. C. Cross, R. M. Hainer, and G. W. King, The asymmetric rotor II: Calculation of dipole intensities and line classification. J. Chem. Phys. 12, 210-243 (1944).

44.

D, G. Burkhard, Factorization and wave functions for the symmetric rigid rotator. J. Mol. Spectry. 2, 187-202 (1958).

45.

W. H. Shaffer, Operational derivation of wave functions for a symmetrical rigid rotator. J. Mol. Spectry. 1, 69-80 (1957); W. H. Shaffer and J. D. Louck, Operational procedure for determination of the matrix elements of the directional cosines for a rigid symmetrical rotator. J. Mol. Spectry. 3, 123-131 (1959).

46.

S. P. Alliluev, On the relation between ``accidental'' degeneracy and ``hidden'' symmetry of a system. Soviet Phys. JETP 6, 156-159 (1958).

47.

R. Loudon, One-dimensional hydrogen atom. Amer. J. Phys. 27, 649-655 (1959).

48.

F. Stevenson, Note on the `Kepler problem' in a spherical space and the factorization method of solving eigenvalue problems. Phys. Rev. 59, 842-843 (L) (1941); L. Infeld and A. Schild, A note on the Kepler problem in a space of constant negative curvature. Phys. Rev. 67, 121-122 (L) (1945).

49.

E. Schrödinger, A method of determining quantum-mechanical eigenvalues and eigenfunctions. Proc, Roy. Irish Acad. Sect. A 45, 9-16 (1940); Further studies on solving eigenvalue problems by factorization. Proc. Roy, Irish Acad. Sect. A 46, 183-206 (1941).

50.

L. Pauling and E. B. Wilson, Jr., ``Introduction to Quantum Mechanics,'' §14. McGraw-Hill, New York, 1935.

51.

J. Bertrand, Théorème relatif au mouvement d'un point attiré vers un centre fixe. C. R. Acad. Sci. Paris 77, 849-853 (1873).

52.

D. F. Greenberg, Accidental degeneracy. Amer. J. Phys. 34, 1101-1109 (1966).

53.

G. Darboux, Étude d'une question relative au mouvement d'un point sur une surface de révolution. Bull. Soc. Math. France 5, 100-113 (1877).

54a.

G. Darboux, Recherche de la loi que doit suivre une force centrale pour que la trajectoire qu'elle détermine soit toujours une conique. C. R. Acad. Sci. Paris 84, 936-938 (1877).

54b.

R. Lehti, Some special types of perturbative forces acting on a particle moving in a central field. Ann. Acad. Sci. Fenn. Ser. A 6, No. 282 (1968).

55.

E. T. Whittaker, ``A Treatise on the Analytical Dynamics of Particles and Rigid Bodies,'' 4th ed. Cambridge Univ. Press, London and New York, reprinted 1961.

56.

J. P. Elliott, Collective motion in the nuclear shell model I. Classification schemes for states of mixed configurations. Proc. Roy. Soc. Ser. A 245, 128-145 (1958).

57.

M. Moshinsky, Soluble many-body problem for particles in a Coulomb potential. Phys. Rev. 126, 1880-1881 (1962).

58.

S. Goshen (Goldstein) and H. J. Lipkin, A simple independent particle system having collective properties. Ann. Physics 6, 301-309 (1959); A simple model of a system possessing rotational states, Ann. Physics 6, 310-318 (1959).

59.

C. G. Darwin, On the diffraction of the magnetic electron. Proc. Roy. Soc. Ser. A 120, 631-642 (1928),

60.

E. H. Kennard, Zur Quantenmechanik einfacher Bewegungstypen. Z. Physik 44, 326-352 (1927).

61.

L. Page, Deflection of electrons by a magnetic field in the wave mechanics. Phys. Rev. 36, 444-456 (1930).

62.

G. E. Uhlenbeck and L. A. Young, The value of 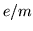$e/m$ by deflection experiments. Phys. Rev. 36, 1721-1727 (1930).

63.

L. Landau, Diamagnetismus der Metalle. Z. Physik 64, 629-637 (1930).

64.

W. Alexandrow, Die magnetische Ablenkung der Korpuskularstrahlen in der Diracschen Wellenmechanik. Ann. Physik (5) 2, 477-484 (1929).

65.

M. S. Plesset, Relativistic wave mechanics of electrons deflected by a magnetic field. Phys. Rev. 36, 1728-1731 (1930).

66.

L. D. Huff, The motion of a Dirac electron in a magnetic field. Phys. Rev. 38, 501-512 (1931).

67.

O. Laporte, The approximation of geometric optics as applied to a Dirac electron moving in a magnetic field. Phys. Rev. 42, 340-347 (1932).

68.

R. F. O'Connell, Motion of a relativistic electron with an anomalous magnetic moment in a constant magnetic field. Phys. Lett. A 27, 391-392 (1968).

69.

I. I. Rabi, Das freie Elektron im homogenen Magnetfeld nach der Diracschen Theorie. Z. Physik 49, 507-511 (1928).

70.

M. H. Johnson and B. A. Lippman, Motion in a constant magnetic field. Phys. Rev. 76, 828-832 (1949).

71.

M. H. Johnson and B. A. Lippman, Relativistic motion in a magnetic field. Phys. Rev. 77, 702-705 (1950).

72.

V. A. Dulock and H. V. McIntosh, Degeneracy of cyclotron motion. J. Math. Phys. 7, 1401-1412 (1966).

73.

T. Sexl, Bemerkung zur Quantelung des harmonischen Oszillators im Magnetfelde. Z. Physik 48, 611-613 (1928); V. Fock, Bemerkung zur Quantelung des harmonischen Oszillators in Magnetfeld. Z. Physik 47, 446-448 (1928).

74.

H. Poincaré, Remarques sur une expérience de M. Birkeland. C. R. Acad. Sci. Paris 123, 530-533 (1896).

75.

J. R. Lapidus and J. L. Pietenpol. Classical interaction of an electric charge with a magnetic monopole. Amer. J. Phys. 28, 17-18 (1960).

76.

G. Nadeau, Concerning the classical interaction of an electric charge with a magnetic monopole. Amer. J. Phys. 28, 566(L) (1960).

77.

B. Lehnert, ``Dynamics of Charged Particles.'' North-Holland Publ., Amsterdam, 1964.

78.

P. A. M. Dirac, Quantised singularities in the electromagnetic field. Proc. Roy. Soc. Ser. A 133, 60-72 (1931).

79.

I. Tamm, Die verallgemeinerten Kugelfunktionen und die Wellenfunktionen eines Elektrons im Felde eines Magnetpoles. Z. Physik 71, 141-150 (1931).

80.

B. O. Grönblom. Über singuläre Magnetpole. Z. Physik 93, 283-285 (1935).

81.

P. Jordan, Über die Diracschen Magnetpole. Ann. Physik 32, 66-70 (1938).

82.

M. N. Saha, The origin of mass in neutrons and protons. Indian J. Math. 10, 141-153 (1936).

83.

H. A. Wilson, Note on Dirac's theory of magnetic poles. Phys. Rev. 75, 309(L) (1949).

84.

J. A. Eldridge, Strings, poles, and the electron. Phys. Rev. 75, 1614-1615(L) (1949).

85.

M. N. Saha, Note on Dirac's theory of magnetic poles, Phys. Rev. 75, 1968(L) (1949).

86.

N. F. Ramsey, Time reversal, charge conjugation, magnetic pole conjugation, and parity. Phys. Rev. 109, 225-226(L) (1958).

87.

M. Fierz, Zur Theorie magnetisch geladener Teilchen. Helv. Phys. Acta 17, 27-34 (1944).

88.

P. P. Banderet, Zur Theorie der singulären Magnetpole. Helv. Phys. Acta 19, 503-522 (1946).

89.

K. W. Ford and J. A. Wheeler, An application of semiclassical scattering analysis. Ann. Physics 7, 287-322 (1959).

90.

E. Goto, On the observation of magnetic poles. J. Phys. Soc. Japan 13, 1413-1418 (1958); Expected behaviour of the Dirac monopole in cosmic space. Prog. Theoret. Phys. 30, 700-718 (1963); E. Goto, H. H. Kolm, and K. W. Ford, Search for ferromagnetically trapped magnetic monopoles of cosmic origin. Phys. Rev. 132, 387-396 (1963).

91.

G. Wentzl, Comments on Dirac's theory of magnetic monopoles. Theoret. Phys. Suppl. 37&38, 163-174 (1966).

92.

Harish-Chandra, Motion of an electron in the field of a magnetic pole. Phys. Rev. 74, 883-887 (1948).

93.

C. J. Eliezer and S. K. Roy, The effect of a magnetic pole on the energy levels of a hydrogen-like atom. Proc. Cambridge Philos. Soc. 58, 401-404 (1962).

94.

W. V. R. Malkus, The interaction of the Dirac monopole with matter. Phys. Rev. 83, 899-905 (1951).

95.

M. Berrondo and H. V. McIntosh, Degeneracy of the Dirac equation with electric and magnetic Coulomb potentials. J. Math. Phys. 11, 125-141 (1970).

96.

J. Schwinger, Magnetic charge and quantum field theory. Phys. Rev. 144, 1087-1093 (1966); Sources and magnetic charge. Phys. Rev. 173, 1536-1554 (1968).

97.

A. Peres, Singular strings of magnetic monopoles. Phys. Rev. Lett. 18, 50-51 (1967); Rotational invariance of magnetic monopoles. Phys. Rev. 167, 1449 (1968).

98.

A. S. Goldhaber, Role of spin in the monopole problem. Phys. Rev. 140, 1407-1414 (1965).

99a.

H. V. McIntosh, Degeneracy of the magnetic monopole. Bull. Amer. Phys. Soc. 12, 699(A) (1967); H. V. McIntosh and A. Cisneros, Motion of a charged particle in the field of a magnetic monopole. Bull. Amer. Phys. Soc. 13, 909 (A) (1968); H. V. McIntosh and A. Cisneros, Degeneracy in the presence of a magnetic monopole. J. Math. Phys. 11, 896-916 (1970).

99b.

D. Zwanziger, Exactly soluble nonrelativistic model of particles with both electric and magnetic charges. Phys. Rev. 176, 1480-1488 (1968); Quantum field theory of particles with both electric and magnetic charges. Phys. Rev. 176, 1489-1495 (1968).

100.

C. Störmer, Periodische Elektronenbahnen im Felde eines Elementarmagneten und ihre Anwendung auf Brüches Modellversuche und auf Eschenhagens Elementarwellen des Erdmagnetismus. Z. Astrophys. 1, 237-274 (1930); Ein Fundamentalprolem der Bewegung einer elektrisch geladenen Korpuskel im kosmischen Raume. Z. Astrophys. 3, 31-52 (1931); Ein Fundamentalproblem der Bewegung einer elektrisch geladenen Korpuskel im kosmischen Raume. II. Z. Astrophs. 3, 227-252 (1931); Ein Fundamentalproblem der Bewegung einer elektrisch geladenen Korpuskel im kosmischen Raume. III. Z. Astrophys. 4, 290-318 (1932); ``The Polar Aurora.'' Oxford Univ. Press (Clarendon), London and New York, 1955.

101.

J. von Neumann and E. Wigner, Behaviour of eigenvalues in adiabatic processes. Physik. Z. 30, 467-470 (1929) (Über das Verhalten von Eigenwerten bei adiabatischen Prozessen).

102.

C. A. Coulson and A. Joseph, A constant of the motion of the two-center Kepler problem. Intern. J. Quantum Chem. 1, 337-347 (1967).

103.

H. A. Erikson and E. L. Hill, A note on the one-electron states of diatomic molecules. Phys. Rev. 75. 29-31 (1949).

104.

S. P. Alliluev and A. V. Matveenko, Symmetry group of the hydrogen molecular ion. Soviet Physics JETP 24, 1260-1264 (1967).

105.

W. Pauli, Jr., Über das Modell des Wasserstoffmolekülions. Ann. Physik 68, 177-240 (1922).

106.

K. M. Case, Singular potentials. Phys. Rev. 80, 797-806 (1950).

107.

(Sir) J. J. Thompson, On the theory of radiation. Philos. Mag. 20, 238-247 (1910).

108a.

J. H. Jeans, On the motion of a particle about a doublet. Philos. Mag. 20, 380-382 (1910).

108b.

(Sir) O. Greenhill, Orbits in the field of a doublet and generally of two centres of force. Philos. Mag. 46, 364-385 (1923).

108c.

L. Page, Three-dimensional periodic orbits in the field of a non-neutral dipole. Philos. Mag. 10, 314-323 (1930).

108d.

M. A. Higab, Three-dimensional motion of an electron in the field of a non-neutral atom. Philos. Mag. 7, 31-52 (1929).

108e.

M. A. Higab, Two-dimensional periodic orbits in the field of a non-neutral [atom]. Philos. Mag. 7, 783-792 (1929).

108f.

M. A. Higab, Periodic orbits in a field of force defined by a certain potential. Philos. Mag. 14, 298-304 (1932).

108g.

M. A. El-Sherbini, Three-dimensional periodic orbits in the field of a non-neutral atom. Philos. Mag. 14, 304-310 (1932).

109.

P. J. Redmond, Generalization of the Runge-Lenz vector in the presence of an electric field. Phys. Rev. B 133, 1352-1353 (1964).

110.

H. A. Bethe and E. E. Salpeter, ``Quantum Mechanics of One- and Two-Electron Atoms.'' Academic Press, New York, 1957.

111.

A. Sommerfeld, Zur Quantentheorie der Spektrallinien. Ann. Physik 51, 1-94, 125-167 (1916).

112.

M. Born, ``The Mechanics of the Atom.'' Ungar, New York, 1960.

113.

A. Galindo and C. Sánchez del Río, Intrinsic magnetic moment as a non-relativistic phenomenon. Amer. J. Phys. 29, 582-584 (1961).

114.

J.-M. Lévy-Leblond, Galilean quantum field theories and a ghostless Lee model, Comm. Math. Phys. 4, 157-176 (1967); Nonrelativistic particles and wave equations. Comm. Math. Phys. 6, 286-311 (1967).

115.

G. Breit, An interpretation of Dirac's theory of the electron. Proc. Nat. Acad. Sci. U.S.A. 14, 553-559 (1928); On the interpretation of Dirac's 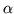$\alpha$-matrices. Proc. Nat. Acad. Sci. U.S.A. 17, 70-73 (1931).

116.

E. Schrödinger, Über die kräftefreie Bewegung in der relativistischen Quantenmechanik. Berliner Ber. pp. 418-428 (1930); Zur Quantendynamik des Elektrons. Berliner Ber. pp. 63-72 (1931).

117.

L. Foldy and S. A. Wouthuysen, On the Dirac spin 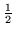$\frac 1 2$ particle and its nonrelativistic limit. Phys. Rev. 78, 29-36 (1950).

118.

T. D. Newton and E. P. Wigner, Localized states for elementary systems. Rev. Modern Phys. 21, 400-406 (1949).

119.

M. H. L. Pryce, The mass-centre in the restricted theory of relativity and its connexion with the quantum theory of elementary particles. Proc. Roy. Soc. Ser. A 195, 62-81 (1949).

120.

M. Cini and B. Touscheck, The relativistic limit of the theory of spin 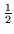$\frac{1}{2}$ particles. Nuovo Cimento 7, 422-423 (1958).

121.

R. P. Feynman and M. Gell-Mann, Theory of the Fermi interaction. Phys. Rev. 109, 193-198 (1958).

122.

L. M. Brown, Two component Fermion theory. Phys. Rev. 111, 957-964 (1958).

123.

G. Temple, The operational wave equation and the energy levels of the hydrogen atom. Proc. Roy. Soc. Ser. A 127, 349-360 (1930).

124.

G. Temple, ``The General Principles of Quantum Theory.'' Methuen, London, 1956.

125.

F. Sauter, Lösung der Diracschen Gleichungen ohne Spezialisierung der Diracschen Operatoren. Z. Physik 63, 803-814 (1930); Zur Lösung der Diraschen Gleichungen ohne Spezialisierung der Diracschen Operatoren, II. Z. Physik 64, 295-303 (1930); Zur Lösung der Dirac-Gleichung fur ein zentralsymmetrisches Kraftfeld. Z. Physik 97, 777-784 (1935).

126.

M. H. Johnson and B. A. Lippman, Relativistic Kepler problem. Phys. Rev. 78, 329 (A) (1950).

127.

E. A. Hylleraas, Zur praktischen Lösung der relativistischen Einelektronengleichungen. Z. Physik 140, 626-631 (1955); Zur praktischen Lösung der relativistischen Einelektronengleichungen, II. Z. Physik 164, 493-506 (1961).

128.

M. Kolsrud, On the solution of Dirac's equation with Coulomb potential. Phys. Norveg. 2, 43-50 (1966).

129.

P. C. Martin and R. J. Glauber, Relativistic theory of radiative orbital electron capture. Phys. Rev. 109, 1307-1325 (1958).

130.

L. C. Biedenharn, Remarks on the relativistic Kepler problem. Phys. Rev. 126, 845-851 (1962).

131.

L. C. Biedenharn, MA11, symmetry considerations in the Dirac-Coulomb problem. Bull. Amer. Phys. Soc. 7, 314 (A) (1962).

132.

L. C. Biedenharn and N. V. V. J. Swamy, Remarks on the relativistic Kepler problem II. Approximate Dirac Hamiltonian having two vector invariants. Phys. Rev. B 133, 1353-1360 (1964).

133.

C. V. Sheth, The relativistic symmetric Hamiltonian and the Foldy-Wouthuysen transformation. Nuovo Cimento A 54, 549-551 (1968).

134.

A. Sommerfeld and A. W. Maue, Approximate adaptation of a solution of the Schrödinger equation to the solution of Dirac's equation. Ann. Physik 22, 629-642 (1935).

135.

H. A. Bethe and L. C. Maximon, Theory of Bremsstrahlung and pair production I. Differential cross section. Phys. Rev. 93, 768-784 (1954).

136.

F. Sauter, Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Dirac's. Z. Physik 69, 742-764 (1931).

137.

O. Klein, Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac. Z. Physik 53, 157-165 (1929).

138.

K. Nikolsky, Das Oszillatorproblem nach der Diracschen Theorie. Z. Physik 62, 677-681 (1930).

139.

I. Postepska, Harmonischer Oszillator nach der Diracschen Wellengleichung. Acta Phys. Polon. 4, 269-280 (1935).

140.

A. Sommerfeld and H. Welker, Künstliche Grenzbedingungen beim Keplerproblem. Ann. Physik 32, 56-65 (1938).

141.

J. von Neumann and E. Wigner, Über merkwürdige diskrete Eigenwerte. Physik Z. 30, 465-467 (1929).

142.

G. N. Stanciu, Further exact solutions of the Dirac equation. J. Math. Phys. 8, 2043-2047 (1967).

143.

N. J. Ionesco-Pallas, Relativistic wave equation for plane motion. Rev. Roumaine Phys. 12 327-336 (1967).

144.

C. A. Coulson and A. Joseph, Self-adjoint ladder operators II. Rev. Modern Phys. 39, 838-849 (1967).

145.

L. Infeld and T. E. Hull, The factorization method. Rev. Modern Phys. 23, 21-68 (1951).

146.

W. Miller, Jr., On Lie algebras and some special functions of mathematical physics. Mem. Amer. Math. Soc. No. 50 (1964); ``Lie Theory and Special Functions.'' Academic Press, New York, 1968; L, Weisner, Group theoretic origin of certain generating functions. Pacific J. Math. 5, 1033-1039 (1955); H. R. Coish, Infeld factorization and angular momentum. Canad. J. Phys. 34, 343-349 (1956).

147.

R. C. Hwa and J. Nuyts, Group embedding for the harmonic oscillator. Phys. Rev. 145, 1188-1195 (1966).

148.

J. Schwinger, ``On Angular Momentum'' (unpublished), reprinted in ``Quantum Theory of Angular Momentum'' (L. C. Biedenharn and H. Van Dam, eds.), pp. 229-279. Academic Press. New York, 1965.

149.

H. Bacry, H. Ruegg, and J.-M. Soriau, Dynamical groups and spherical potentials in classical mechanics. Comm. Math. Phys. 3, 323-333 (1966).

150.

M. Luming and E. Predazzi, Theory of 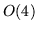$O(4)$ invariant potentials and its application to a short-range example. Ann. Physics 40, 221-236 (1966); A set of exactly soluble potentials. Nuovo Cimento B 41, 210-212(L) (1966).

151.

N. Mukunda, Realizations of Lie algebras in classical mechanics. J. Math. Phys. 8, 1069-1072 (1967); Dynamical symmetries and classical mechanics. Phys. Rev. 155, 1383-1386 (1967); N. Mukunda, L. O'Raifeartaigh, and E. C. G. Sudarshan, Characteristic noninvariance groups of dynamical systems. Phys. Rev. Lett. 15, 1041-1044 (1965).

152.

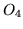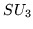D. M. Fradkin, Existence of the dynamical symmetries $O_4$ and $SU_3$ for all classical central potential problems. Progr. Theoret. Phys. 37, 798-812 (1967).

153.

G. Maiella and B. Vitali, A note on dynamical symmetries of classical systems. Nuovo Cimento A 47, 330-333 (1967).

154.

J. Rosen, On realizations of Lie algebras and symmetries in classical and quantum mechanics. Nuovo Cimento A 49, 614-621 (1967).

155.

V. A. Dulock and H. V. McIntosh, On the degeneracy of the Kepler problem. Pacific J. Math. 19, 39-55 (1966).

156.

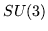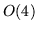D. G. Ravenhall, R. T. Sharp, and W. J. Pardee, A connection between $SU(3)$ and $O(4)$. Phys. Rev. 164, 1950-1956 (1967).

157.

M. Y. Han and P. Stehle, 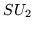$SU_2$ as a classical invariance group. Nuovo Cimento 48, 180-187 (1967).

158.

A. Cisneros and H. V. McIntosh, Symmetry of the two-dimensional hydrogen atom. J. Math. Phys. 10, 277-286 (1969).

159.

P. Stehle and M. Y. Han, Symmetry and degeneracy in classical mechanics. Phys. Rev. 159, 1076-1082 (1967).

160.

L. Susskind and J. Glogower, Quantum mechanical phase and time operator. Physics 1, 49-61 (1964); P. Carruthers and M. M. Nieto, Coherent states and the forced quantum oscillator. Amer. J. Phys. 33, 537-544 (1965); F. Teissier du Cros, An attempt towards the definition of the phase of quantum oscillators. Z. Angew. Math. Phys. 16, 16 (1965); P. Carruthers and M. M. Nieto, Phase and angle variables in quantum mechanics. Rev. Modern Phys. 40, 411-440 (1968); E. C. Lerner, Harmonic oscillator phase operators. Nuovo Cimento B 56, 183-186(L) (1968).

March 19, 2002