next up previous contents
Next: About this document ... Up: Second Level Triflexagon Cutouts Previous: Tukey triangles

Flexagon permutations


  
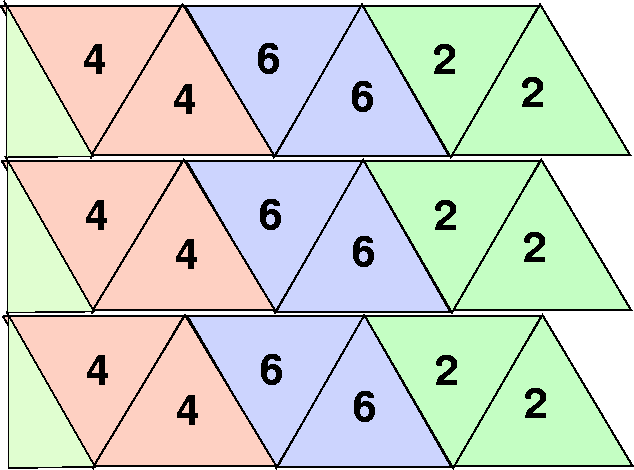
Figure 28: Left: Permutation of the triangles along the strip for a second level normal flexagon.
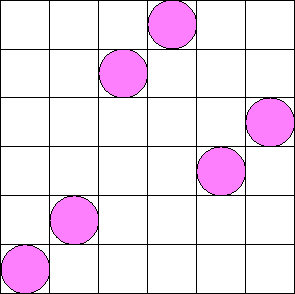\begin{figure} \centering \begin{picture} (200,220) \put(3,0){\epsfxsize=200pt \epsffile{2ndgraf.eps}} \end{picture} \end{figure}


  
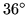Figure 29: Top side of the second level $36^\circ-36^\circ-108^\circ$ triangle cutout. Together with its backside, the figure displays one single flexagon with five sectors, the minimumum requirement to lie flat on account of the $36^\circ$ angle.
\begin{figure} \centering \begin{picture} (390,520) \put(0,0){\epsfxsize=390pt \epsffile{s3636108top.eps}} \end{picture} \end{figure}


  
Figure 30: Bottom side of the second level 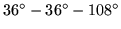$36^\circ-36^\circ-108^\circ$ triangle cutout.
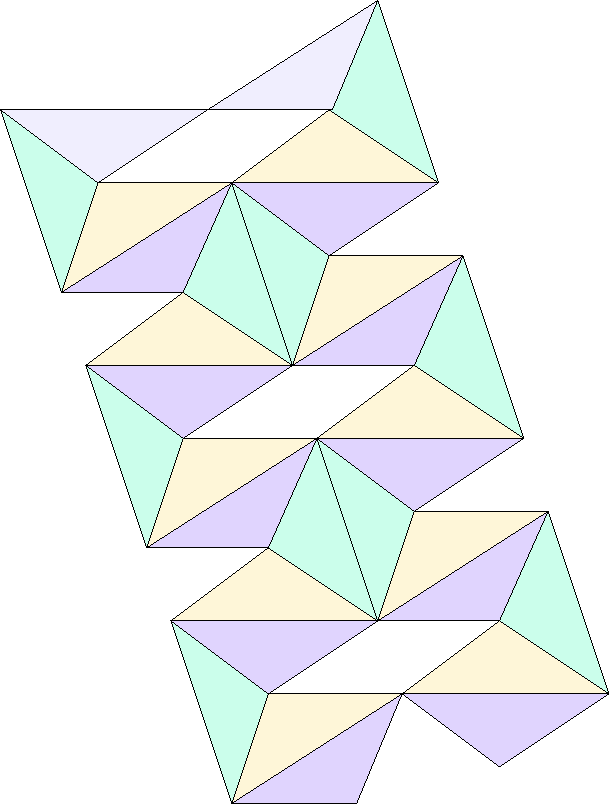\begin{figure} \centering \begin{picture} (390,510) \put(0,0){\epsfxsize=390pt \epsffile{s3636108bot.eps}} \end{picture} \end{figure}


  
Figure 31: Bottom side of three sectors of the second level normal triflexagon cutout. Together with its backside, the figure makes one single triflexagon because three sectors are needed to make it lie flat.
\begin{figure} \centering \begin{picture} (406,460) \put(0,0){\epsfxsize=406pt \epsffile{secondtop.eps}} \end{picture} \end{figure}


  
Figure 32: Bottom side of three sectors of the second level normal triflexagon cutout. Together with its backside, the figure makes one single triflexagon because three sectors are needed to make it lie flat.
\begin{figure} \centering \begin{picture} (406,450) \put(0,0){\epsfxsize=406pt \epsffile{secondbot.eps}} \end{picture} \end{figure}

next up previous contents
Next: About this document ... Up: Second Level Triflexagon Cutouts Previous: Tukey triangles
Microcomputadoras
2000-11-01