next up previous contents
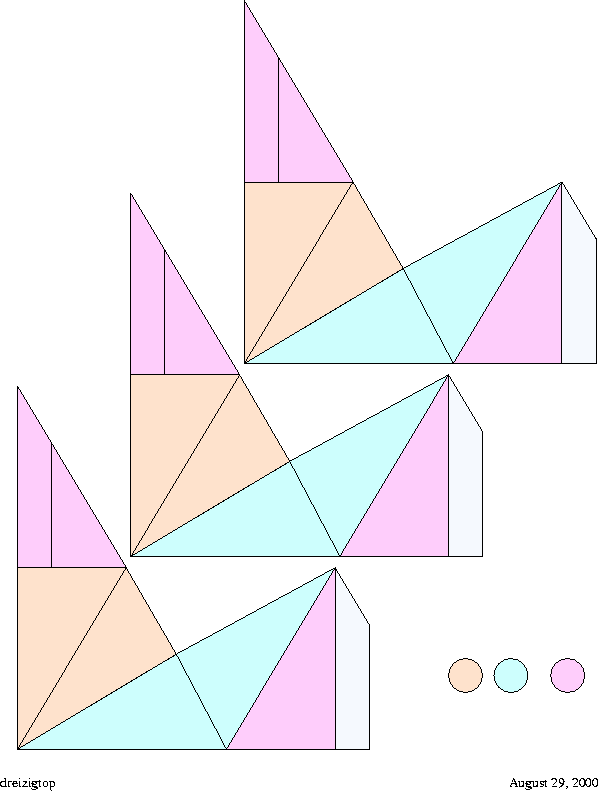
Next: Binary Triflexagon Cutouts Up: First Level Triflexagon Previous: Tukey triangle

Flexagon permutations


  
Figure 8: Permutation of the triangles along the strip for a normal triflexagon. They run in order, subject to being flipped over, so the permutation is the identity.
\begin{figure} \centering \begin{picture} (140,140) \put(0,0){\epsfxsize=140pt \epsffile{1stgraf.eps}} \end{picture} \end{figure}


  
Figure 9: Top side of the 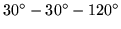$30^\circ-30^\circ-120^\circ$ triangle cutout. Together with its backside, the figure displays one single flexagon with six sectors, the minimumum requirement to lie flat on account of the 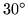$30^\circ$ angle.
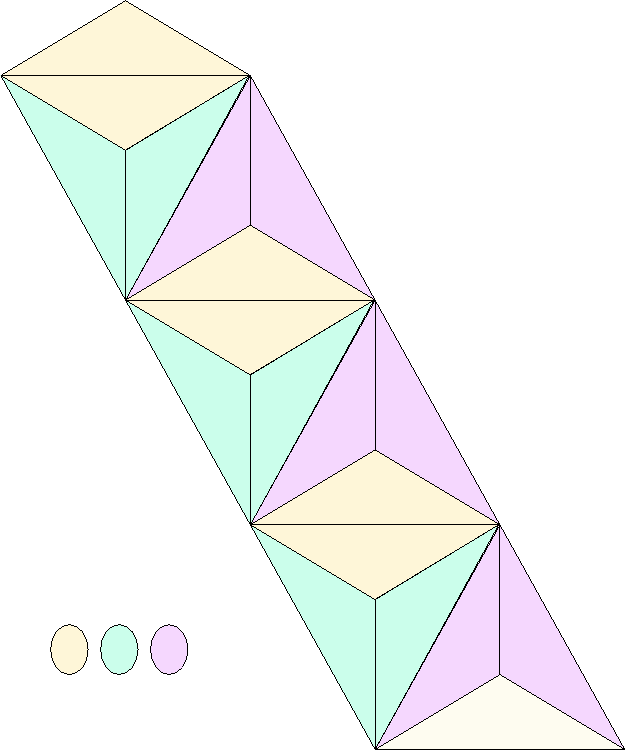\begin{figure} \centering \begin{picture} (400,490) \put(0,0){\epsfxsize=400pt \epsffile{3030120top.eps}} \end{picture} \end{figure}


  
Figure 10: Bottom side of the 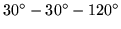$30^\circ-30^\circ-120^\circ$ triangle cutout.
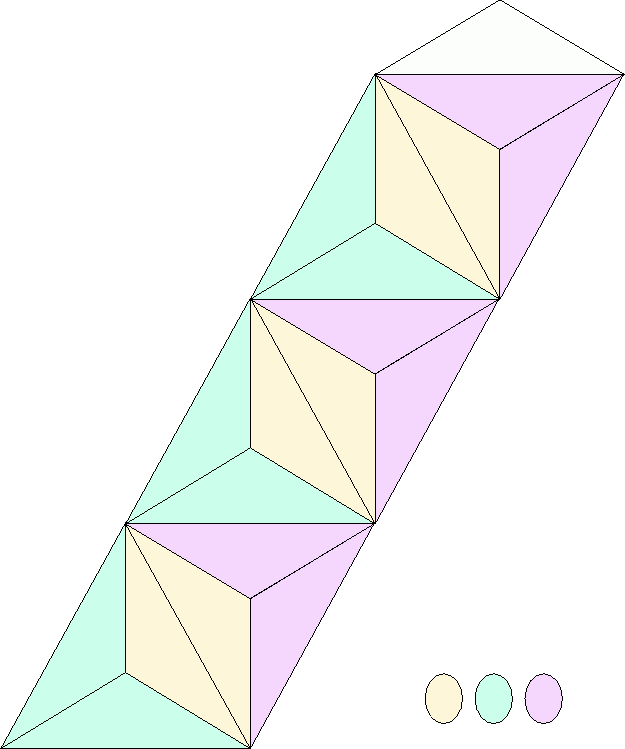\begin{figure} \centering \begin{picture} (400,470) \put(0,0){\epsfxsize=400pt \epsffile{3030120bot.eps}} \end{picture} \end{figure}


  
Figure 11: Top side of the 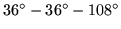$36^\circ-36^\circ-108^\circ$ triangle cutout. Together with its backside, the figure displays one single flexagon with five sectors, the minimumum requirement to lie flat on account of the 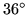$36^\circ$ angle.
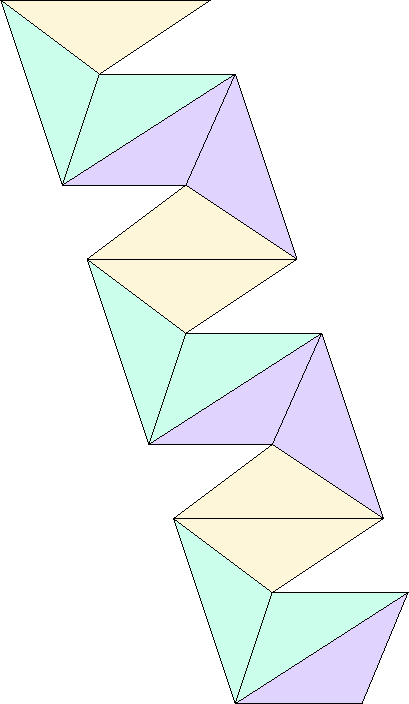\begin{figure} \centering \begin{picture} (450,470) \put(0,0){\epsfysize=450pt \epsffile{3636108top.eps}} \end{picture} \end{figure}


  
Figure 12: Bottom side of the 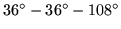$36^\circ-36^\circ-108^\circ$ triangle cutout.
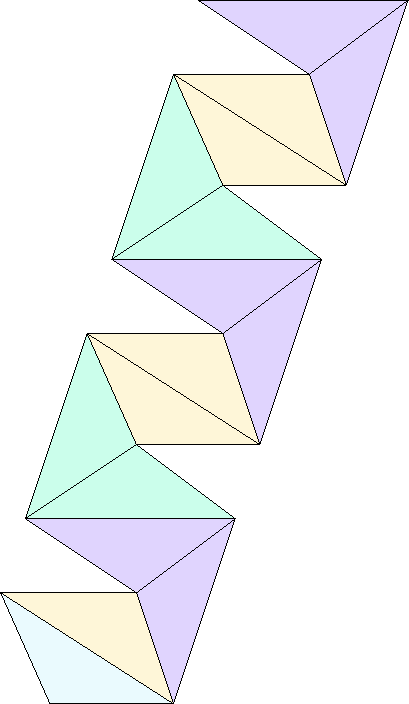\begin{figure} \centering \begin{picture} (450,450) \put(0,0){\epsfysize=450pt \epsffile{3636108bot.eps}} \end{picture} \end{figure}


  
Figure 13: Top side of the 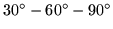$30^\circ-60^\circ-90^\circ$ triangle cutout. Together with its backside, the figure displays one single flexagon with six sectors, the minimumum requirement to lie flat on account of the 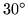$30^\circ$ angle.
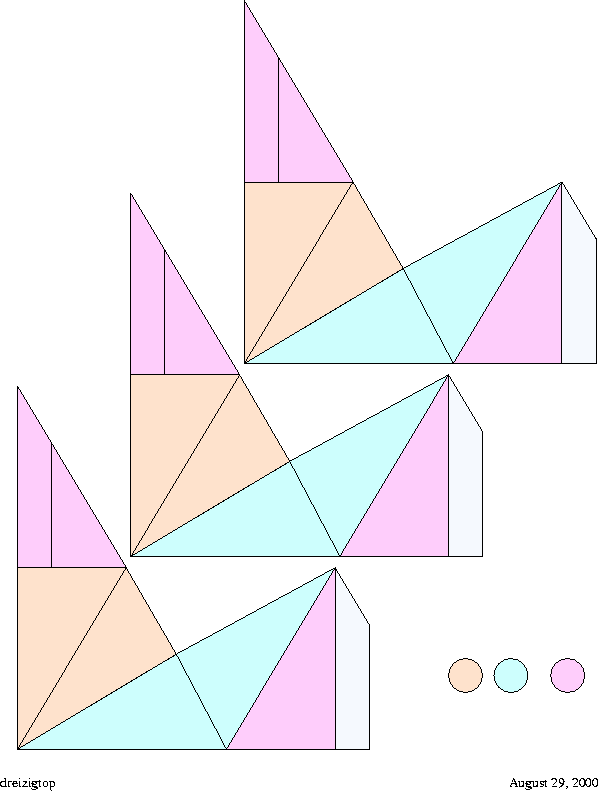\begin{figure} \centering \begin{picture} (390,515) \put(0,0){\epsfxsize=390pt \epsffile{dreizigtop.eps}} \end{picture} \end{figure}


  
Figure 14: Bottom side of the 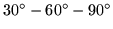$30^\circ-60^\circ-90^\circ$ triangle cutout.
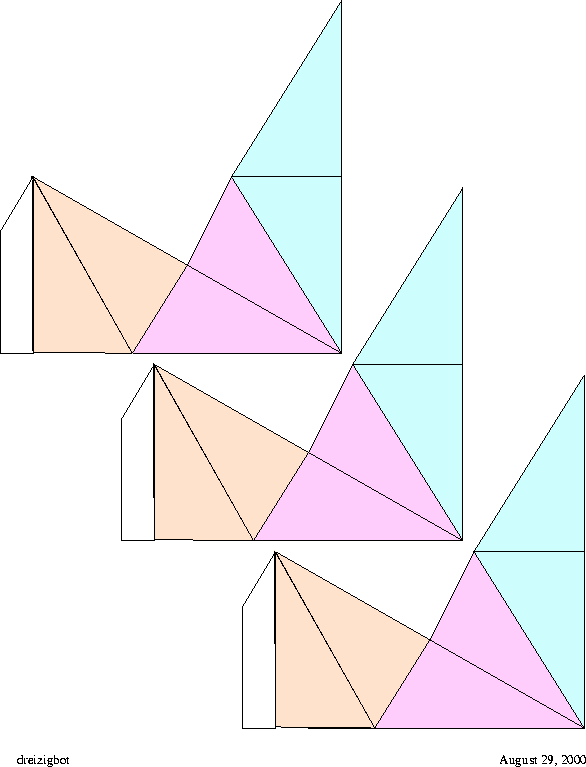\begin{figure} \centering \begin{picture} (390,485) \put(0,0){\epsfxsize=390pt \epsffile{dreizigbot.eps}} \end{picture} \end{figure}


  
Figure 15: Top side of the 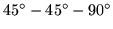$45^\circ-45^\circ-90^\circ$ triangle cutout. Together with its backside, the figure displays one single flexagon with four sectors, the minimumum requirement to lie flat on account of the 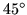$45^\circ$ angle.
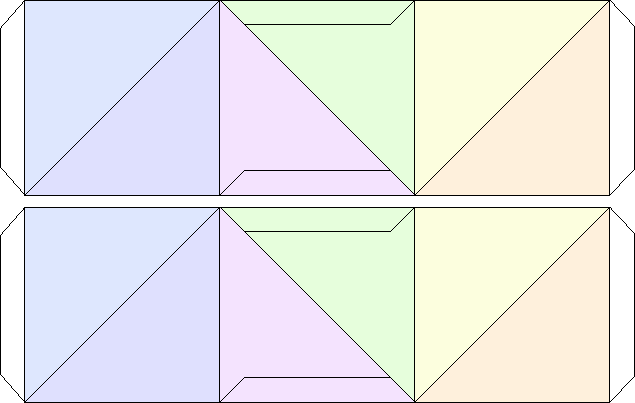\begin{figure} \centering \begin{picture} (406,300) \put(0,0){\epsfxsize=406pt \epsffile{neunzigtop.eps}} \end{picture} \end{figure}


  
Figure 16: Bottom side of the $450^\circ-45^\circ-90^\circ$ triangle cutout.
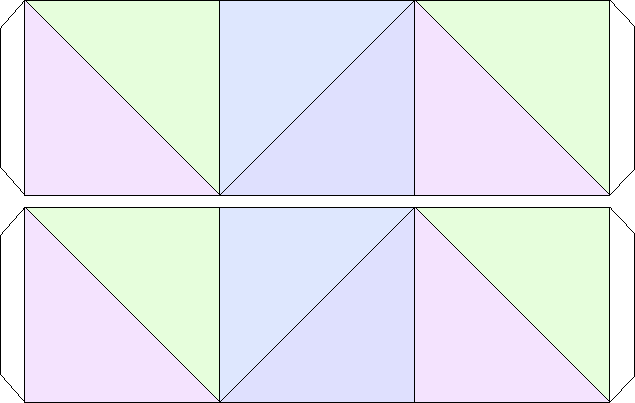\begin{figure} \centering \begin{picture} (406,300) \put(0,0){\epsfxsize=406pt \epsffile{neunzigbot.eps}} \end{picture} \end{figure}


  
Figure 17: Top side of the first level normal triflexagon cutout. Together with its backside, the figure contains one single triflexagon.
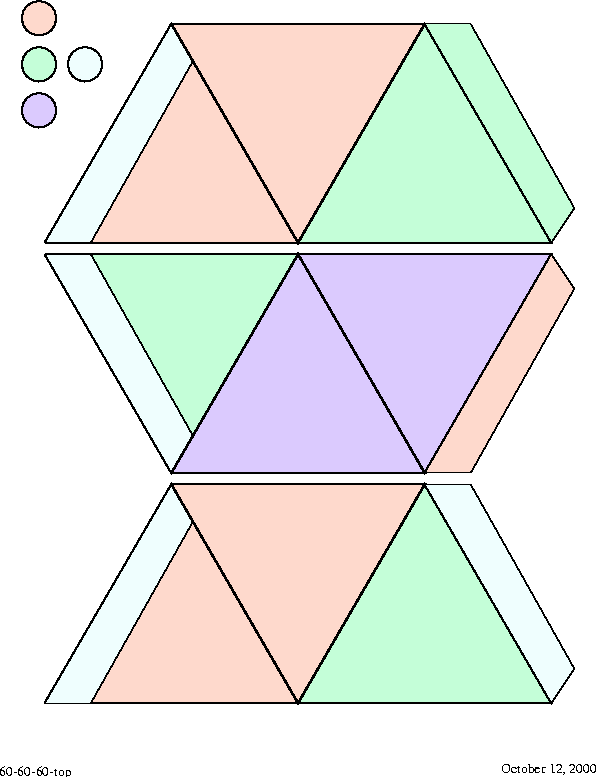\begin{figure} \centering \begin{picture} (390,480) \put(0,0){\epsfxsize=390pt \epsffile{60-60-60top.eps}} \end{picture} \end{figure}


  
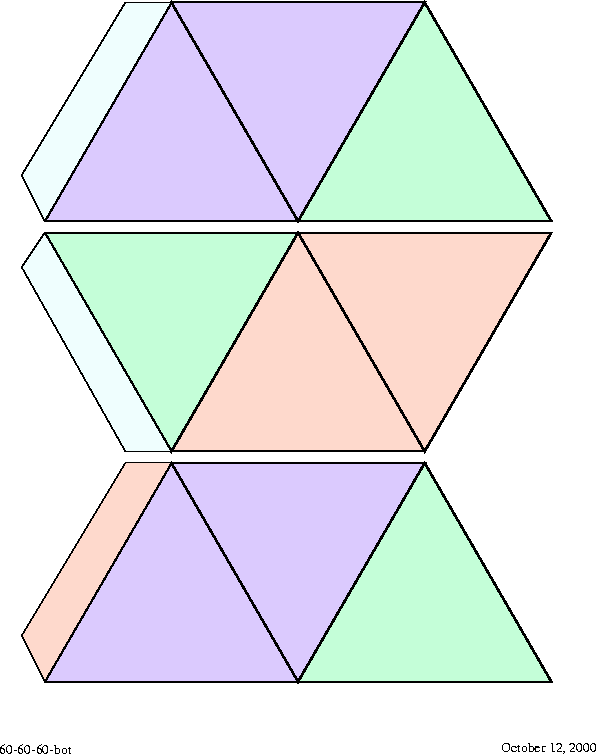
Figure 18: Bottom side of the first level normal triflexagon cutout. Together with its backside, the figure contains three triflexagons.
\begin{figure} \centering \begin{picture} (390,483) \put(0,0){\epsfxsize=390pt \epsffile{60-60-60bot.eps}} \end{picture} \end{figure}

next up previous contents
Next: Binary Triflexagon Cutouts Up: First Level Triflexagon Previous: Tukey triangle
Microcomputadoras
2000-11-01