Reversible automata

Another construction in the cartesian product of state spaces yields automata whose evolution can be reversed; it is based on ideas originating with Edward Fredkin. This time we need just one rule, , with which the following composite rule of evolution can be created:

This definition has a leftward orientation, with an entirely similar definition leaning to the right. Likewise, the exclusive or could be replaced by any other invertible function; for binary automata the only alternative would be the exclusive nor.

To undo the evolution, consider the evolution of three successive cells:

we would like to recover the state from the second line. Although a is readily available, it is necessary to liberate b from the combination . Given that both a and c are available, can be calculated, then used to release b from the invertible combination in which it is bound.

Altogether this is a process embodied in the rule

which must be the rule which will reverse the evolution resulting from the application of the first.

To apply these ideas in two dimensions, consider the following layout:

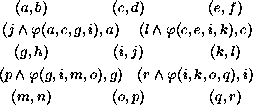
wherein the rule of evolution is evidently

As before, there is enough information in the second generation cells surrounding the first generation cell to recover ; the appropriate rule is:

Again following the one dimensional case, these definitions can be oriented toward different directions, just as the connective can be assigned different meanings. Such variants do not necessarily yield all possible invertible rules; historically very few were known until Fredkin proposed ``second order'' rules, of which these are a variant.

Every binary rule leads to a distinct pair of reversible quaternary rules (some of which may be self-reversible, and some pairs of which may have been generated by a pair of binary rules), even when the binary rule itself is not reversible; there are also cases in which the binary rule was already reversible.

---

Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx