A master diagram

Evidently the subdiagram consists of two disjoint loops; the first, of length 1, leads to an unending sequence of zeroes while the second, of length 2, leads to an alternating sequence of zeroes and ones. These are exactly the still life configurations for this rule.

Perhaps it is worth emphasizing the point that there are many diagrams which can be associated with a cellular automaton, a significantly large proportion of which are subdiagrams of a de Bruijn diagram. Many of the remainder are associated with extensions of de Bruijn diagrams; altogether de Bruijn diagrams constitute a central reference point in a context that might have seemed to be open to any arbitrary kind of diagram.

The literature of automata theory shows varying degrees of awareness of the diagram; much contains intuition that was never formalized, but as time passes references have become more centralized and specific. For example, there are treatments of automata in terms of formal language theory [10,11] which refer to ``regular expression diagrams,'' which are recognizable as subdiagrams of a de Bruijn diagram. Masakazu Nasu [12] refers to them by name and invokes their properties; Erica Jen [13] refers to them, and it is likely that a diligent search would turn up still further instances of their use.

By using longer neighborhoods, the results of more than one generation of evolution may be incorporated in the criterion defining the subdiagram. In that way arbitrary combinations of shifts and periodicities may be studied, not to mention even more elaborate combinations. The following list mentions some of the additional possibilities.

  1. evolution to a constancy after n generations.
  2. evolution of the cells of binary automaton into their complements; permutation of the values of the cells of an arbitrary automaton.
  3. a quiescent state is one which does not change when its entire neighborhood is quiescent; a nilpotent rule (of order n) is one for which all cells become quiescent after n generations.
  4. a configuration is idempotent (of order n) if, for the 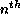generation and thereafter, the values of its cells do not change. A rule is idempotent if all configurations are idempotent.
  5. a configuration is superluminal if it shifts a distance greater than the radius of the neighborhoods in each generation.



Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx