Three stage binary matrix

 
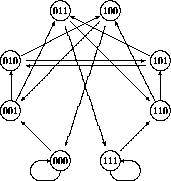
Figure 10: Generic (2,3/2) de Bruijn diagram.  

By the third stage the staircase is fully evident; each step contains k 1's, likewise there are k staircases:

0.30em

The minimal equation is readily determined to be , and as before the Jordan normal form prevails.

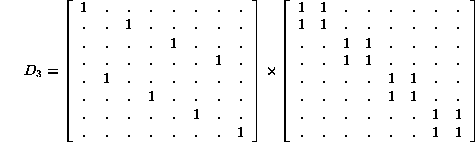
There are two interesting factorizations, both of which are quite general: according to

0.30em

and according to 0.30em

Several relationships among these matrices are evident; for example:

wherein I is the unit matrix. The factors satisfy several identities, of which the most useful are:

P and Q are noncommuting permutation matrices; nevertheless the noncommutative binomial theorem can still be used to evaluate powers of D. Whatever scheme is used, the essential observation is that powers of D exhibit broader steps and more numerous ladders until the matrix is solidly filled with 1's; from then on successive powers merely differ by the factor k.

---

Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx