Topological matrix
The topological matrix 
is defined by
The most important application of the topological matrix consists in the fact that its powers describe paths between nodes containing multiple links, according to the power involved. Since the elements of such matrices are integers the powers are useful for counting total numbers of paths, but not to classifying the paths into different categories. The reason for this is apparent from examining the definition of matrix multiplication,
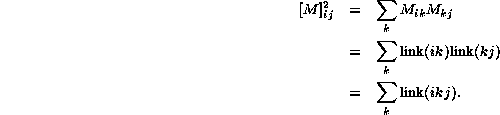
Diagonal elements of this matrix count loops; the trace yields the total number of loops, counting each of them once for every node which they contain. Thus
is a generating function for the prime loop count. By prime loop is meant one for which
portions of the loop are not retraced. By using a determinantal identity for the matrix
exponential, it is possible to obtain a generating function involving the characteristic
equation of M (and using a matrix version of 
).
where n is the dimension of M and 
is its characteristic polynomial. Actually this is a variant definition of the
characteristic polynomial, often seen in integral equation theory; by associating t
with M rather than I the limit of large n is better behaved.
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx