Formal definition.

The indexing shown is one of convenience for visual display, but a more mathematical arrangement would be to use n-bit binary numbers as indices. The bit of the index would be 0 or 1 according to whether the node is included in the subset or not. With such symbolism the remaining rows could be explicitly constructed from those associated with the unit classes.

Even without this element of sophistication, the rule of formation of the subset matrix is easily described. Begin with the observation that the fundamental requirement for the definition of any function is that each argument has just one image. Links in a graph define a function when there is just one link of a given class leading onward from a given node; the subset diagram is created when this condition is violated, by combining multiple links into a single link between subsets.

Even though the linkage of a given graph does not define a function, the subset linkage is always functional and, thanks to the inclusion of the null set as a destination, defined for the entire subset graph. Each class of links defines one function, say or . The subset diagram describes the union , which itself is not functional.

Let a and b be nodes, S a subset, and |S| the cardinality of S; then

---

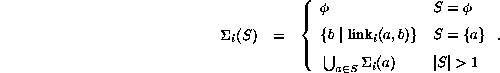
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx