Evolution matrices
The multiplication of ordinary symbolic matrices follows the algebra of regular expressions; that is, multiplication concatenates symbols, union (addition) offers alternatives, the empty set acts like zero.
Moreover the 
power of a matrix M
contains all the possible words of length n, distributed throughout the matrix
according to the overlap of the indices of constituent letters as chains are built up to
length n. All this overlap in 
is no longer
explicit, yet its matrix elements are still indexed by their initial and final partial
neighborhoods.
To track the evolution of a configuration consider the following variant of Eq. 8, which describes the evolution of individual neighborhoods:
which can be decomposed into the sum
by defining
As an example, for Rule 22 0.30em
decomposable into the two matrices 0.30em
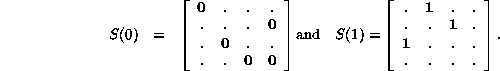
Altogether, we see that 0 has five counterimages, 1 only three. From the
product 
, 0.30em
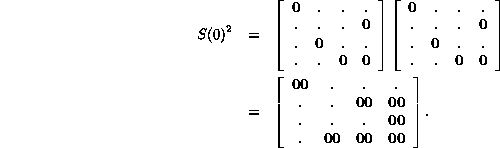
the string 00 is seen to have seven counterimages, and so on for all the other configurations.
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx