Partitioned pair matrix

The tensor product of the connectivity matrices of two diagrams is the connectivity matrix of their cartesian product, wherein pairs of nodes are linked according to whether both members of the pair are each linked in their own diagram. Sometimes a careful arrangement of the nodes in the tensor product will partially diagonalize the connectivity matrix, rendering some property of the arrangement more evident than it would otherwise have been.

A case in point consists in grouping all the pairs composed of equal elements together in a subset , and the rest into the subset . It then becomes evident whether links in a tensor square describe pairs of links in the original diagram which have a node in common by linking to or the reverse, both nodes in common by linking to , or neither by linking to .

Partition accordingly

and consider the eigenvalue equation with a similarly partitioned eigenvector

The following submatrix equations are the result:

If is already an eigenvalue belonging to P, it follows that Qy=0; whether this requires that Q=0 depends somewhat on S, but the condition is quite sufficient. If is not an eigenvalue of S, is invertible whence and would have to be singular unless y were 0.

Consideration of a left eigenvector leads to similar conclusions regarding , while if is an eigenvalue of S as well as P, Rx must vanish. Broadly speaking, if either of the diagonal submatrices already has the eigenvalue, it had better be decoupled from the other, but the details of the uncoupling can get messy.

In practice, another line of reasoning is slightly more compact. Consider

If P were a de Bruijn matrix it would be an irreducible nonnegative matrix and would have a maximum eigenvalue strictly larger than unless QR=0; Q=0 or R=0 would be sufficient. In any event, continuing shows that

with

Gradually the series of requirements

develops, which can be summed to recover

 

The very slightly stronger result is due to the additional knowledge about P.

To illustrate this result with respect to the three rules of Sec. 8, rearrange the indices of the matrix N to group paired indices and then complementary indices ; we obtain

0.45em

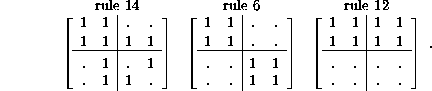
The off diagonal submatrices for Rule 14, for which , force an eigenvalue larger than the minimum, whereas the other two matrices are partially diagonal and maintain the minimum value. Rule 6 is self-complementary, as evidenced by the equality of its diagonal submatrices P and S.

---

Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx