A (2,1) example

The only reversible rules for (2,1) automata are trivial, but nevertheless still instructive. Consider Rule 204, whose evolution is stasis,

0.45em

These matrices are not permutation matrices nor even stochastic, since neither row sums nor column sums are constant. Nevertheless they are idempotent and generate a semigroup of four matrices of similar appearance, namely with the multiplication table

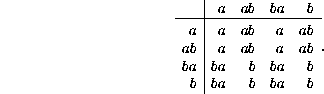
Consequently, every product has four counterimages, seemingly contradicting the claimed uniqueness. However, we need to form new symbolic matrices, which show the ancestral cell rather than the evolved cell; this ancestral cell is the central cell of the ancestral neighborhood, which can be read off from the indices of the de Bruijn matrix.

For Rule 204, these matrices are

0.45em

they already display the crucial property: every counterimage of 0 is 0, whilst every counterimage of 1 is 1. Therefore Rule 204 is invertible by a (2,0) automaton, which is not surprising since it is really a radius zero automaton itself. Trivial in the present instance, the property is once again: there exists some word length r for which every word in the product of r 's and 's has the same central symbol. For this to work r must be odd, but inversion could be combined with shifting so that shift inverses also exist.

---

Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx