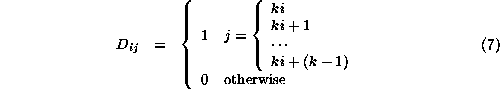De Bruijn diagrams
By a de Bruijn diagram [23] one understands a graph whose nodes are sequences of symbols from some alphabet, for example the set of states of an automaton. The sequences all have the same length, often called the number of stages because of an application to shift register theory [24]; for automata they are partial neighborhoods. In one dimension, a single cell could be dropped from one end or the other of a given neighborhood, although other decompositions are conceivable (dropping or adding two cells, say).
Many authors have used de Bruijn diagrams to study cellular automata, among them Nasu [8], Erica Jen [25], Wentian Li [26], and Wolfram [27]. There does not seem to be any evidence of an attempt to formulate two-dimensional de Bruijn diagrams.
The nodes of a de Bruijn diagram are linked according to their overlap, resulting in a map which reveals the possible succession of contents in a moving window as it advances across an even longer sequence. For automata, the most convenient choice of window size --- the number of stages --- is the length of a full neighborhood, that being the basic unit participating in the evolutionary process.
A de Bruijn diagram is also represented by its connectivity matrix; for this purpose it
is convenient to represent the states of a 
automaton by the digits 0, 1, 
k-1,
its partial neighborhoods by 2r-digit numbers radix k. Multiplication by k
shifts cells, arithmetic modulo 
drops the
leftmost cell, adding a single digit number adjoins a new rightmost cell; altogether
As an example, 
automata have four different
partial neighborhoods 00, 01, 10, and 10, overlapping each
other to form eight full neighborhoods of three cells each. Regarding these binary strings
as numerical indices produces
0.30em
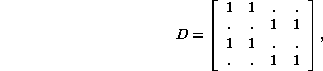
wherein dots replace zeroes for clarity.
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx