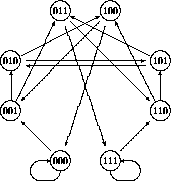
Figure 10: Generic (2,3/2) de Bruijn diagram.
By the third stage the staircase is fully evident; each step contains k 1's, likewise there are k staircases:
0.30em
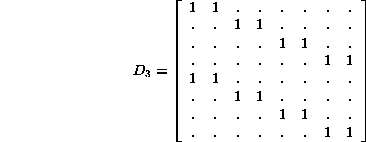
The minimal equation is readily determined to be 
,
and as before the Jordan normal form prevails.
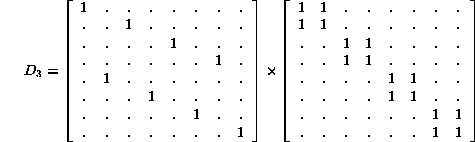
There are two interesting factorizations, both of which are quite
general: 
according to
0.30em
and 
according to
0.30em
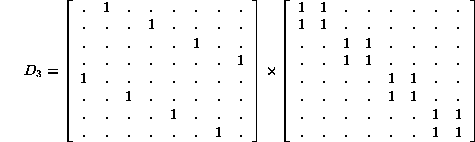
Several relationships among these matrices are evident; for example:
wherein I is the unit matrix. The factors satisfy several identities, of which the most useful are:
P and Q are noncommuting permutation matrices; nevertheless the noncommutative binomial theorem can still be used to evaluate powers of D. Whatever scheme is used, the essential observation is that powers of D exhibit broader steps and more numerous ladders until the matrix is solidly filled with 1's; from then on successive powers merely differ by the factor k.