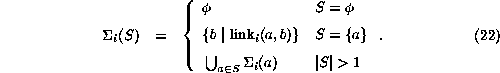
The nodes are grouped into subsets, note being taken of the subsets to which one can arrive through systematic departures from all the nodes in any given subset. The result is a new graph, with subsets for nodes and links summarizing all the places that one can get to from all the different combinations of starting points. Sometimes, but far from always, the possible destinations narrow down as one goes along; in any event one has all the possibilities cataloged.
One point to be observed is that if one thinks that there should be a link at a certain node and there is not, the link should be drawn to the empty set instead; a convention which assures every label of having a representation at every node in the subset diagram.
Let a and b be nodes in a given diagram, S a subset, and |S| the cardinality of S; then the formal definition of its subset diagram is
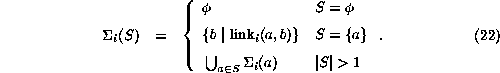
There is another important reason for working with subsets. Labelled links resemble functions, by associating things with one another. But if two links with the same label emerge from a single vertex, they can hardly represent a function. Forging the subset of all destinations, leaves one single link between subsets, bringing functionality to the subset diagram even though it did not exist originally. Including the null set ensures that every point has an image, avoiding partially defined functions.
Once the subset diagram has been formed, if a path leads from the universal set to the empty set, that is conclusive evidence that such a path exists nowhere in the original diagram. Another application---the one originally envisioned by Moore---is to determine whether there are paths leading to the unit classes. Such a paths, if they existed, could be used to force an automaton into a predetermined state, no matter what its original condition.