A doubly stochastic one-stage de Bruijn diagram would have a probability matrix
with q = 1 - p, whose eigenvalues would be 
;
being symmetric, the matrix of both left and right eigenvectors would be
The probability matrix of a two stage diagram is a little more complicated.
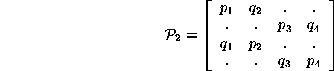
with 
and the characteristic polynomial
with two determinants defined by
The determinant of the de Bruijn matrix is the product of two smaller determinants corresponding to the evident blocks in the de Bruijn matrix; in this we have a special case of a quite general result. The p's and q's were defined as they are with the thought of equating the subscript pairs (1,2) and (3,4) to get a doubly stochastic matrix, but the best interpretation of the vanishing of the small determinants is that the biases of the probabilities in their submatrices are equal.
The constant term in the characteristic equation will be zero, giving a
single zero root, if either determinant is zero. The coefficient of
will also be zero if both are zero, producing a double zero
root. In order to get three equal roots and thus open up the
possibility of the Jordan normal form, requires some similarity between
the two submatrices in addition.
The representations of the de Bruijn matrix as sums and products need very little change to apply to the probabilistic versions as well. The factorizations give immediate formulas for determinants; when they do not vanish, the block diagonal form of of one of the factors, together with the fact that the other is a permutation matrix quickly reveals a form for the inverse matrix. Taking as an example the matrix of the last section, we have
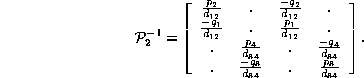
The Gerschgorin limit of this matrix requires its maximum eigenvalue to
be less than the greatest reciprocal determinant 
or
(all with respect to absolute values). Generalizing, this
means that every eigenvalue of 
must be greater than
the lesser of these determinants. Of course, if one of them is zero, we
know that the lower bound is reached and 
is singular.
In the other direction, unless some 
or 
is zero, every
matrix element of 
will be strictly positive,
although in the probabilistic case no two of them have to be equal.
This ensures that the maximum eigenvalue, 
, will be
unique. Conversely, if some probability or coprobability vanishes, the
possibility of degeneracy exists (but is not obligatory).