One of the fundamental conclusions of automata theory is that finite automata or those which are effectively finite, such as the cyclic configurations of an infinite automaton, eventually fall into periodic behavior. Generally the only way to discover these periods is by exhaustive enumeration, according to which the evolution of every possible initial configuration is followed out until the first repetition of a previous configuration is observed.
The notation 
means that the configuration repeats itself
after 
generations, but that there are only 
different
phases, variations of which can occur through rotation or reflection.
Accordingly the representative configuration shown is the one with a
gap of maximal length, which is always placed at the extreme right.
If a shift to the right of 
cells is involved, the notation
is used; a reflective symmetry is often associated
with 
.
On general principles a ring of N cells cannot have a cycle longer
than 
, but in practice the lengths of the cycles grow at a far
slower rate with increasing N. Some of the longest cycles are a
consequence of a shift, whose least common multiple with N often
results in a far longer period than the time required to simply repeat
the pattern.
Likewise, the periods are determined by the lengths of possible loops
in a de Bruijn diagram of 
nodes, which limits the maximum length
of a primitive period to this value. In practice this is also found to
be a generous upper limit.
The results can be summarized in a table of periods versus cycle lengths. The columns correspond to torii of fixed circumference, the rows to fixed periods, the values of both of which are stated in the margins. The first twenty periods are shown below.
0.1em
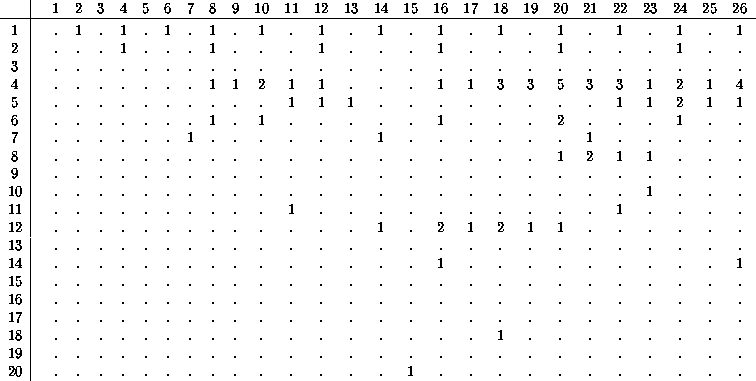
There is only a single still life, a single configuration of period two, and none at all of period three.
From the table above and the continuation below it will be seen that there are numerous configurations of periods 4, 12, and 28. They belong to an extensive family which is formed by the expansion of isolated live cells, and which contains many more members besides. Isolated cells, in Rule 22 especially, follow a growth pattern which resembles a binary counter, or a fractal as the image would be classified nowadays. The boundary of a region filled with live cells expands into the gap separating such regions, but periodically the interior of the expanding region dies out.
Thus if a pair of cells are allowed to expand around a ring, a complementary configuration may be created when the expanding frontiers have nearly met but the expanding region has just become vacant. If the symmetry is just right the complement will repeat the performance to recreate the original configuration, setting the stage for a repetitive cycle.
The final fourteen periods are shown in the table below; as before columns correspond to the circumference of the ring, rows to a fixed period.
0.1em
Longer rings might have been attempted were it not for the fact that the computing time required to analyze the ring doubles with every increment in length, leaving N=34 as something of a limit of endurance with present equipment and techniques. A few additional increments could be gained by using faster equipment, and by proving some ``gap theorems'' which would render unnecessary the analysis of a certain fraction of cases.
Nevertheless, in practice the interval 
provided
enough special cases that it was possible to discover several general
families of configurations, finally leading to the analysis of periods
in terms of de Bruijn diagrams.