Amongst the variety of transformations which can change the appearance of cellular automata are those which modify the neighborhoods. For example, it is possible to show that linear cellular automata do not need to have large neighborhoods; in fact, as Albert and Culick [3] showed,it is sufficient to have just two cells in a neighborhood. The essential idea is to replace the entire neighborhood by a single cell; of course the new cell must have enough states to describe every possible content of the original neighborhood.
Even if the cells are grouped in clusters, there will still be some interaction at the boundary, so that a new rule of evolution has to be devised. Also, since the interaction has to be one-sided if there are only pairs of cells in the new neighborhood, the original two-sided interactions can be recovered by extracting information from alternate generations. Since three cells would form a second generation neighborhood, it can be contrived that we think of the central cell as evolving, rather than one of the edge cells.
Thus, for lack of a better notation, let us define a 
automaton A with the rule 
in terms of a given 
automaton
a whose rule of evolution is 
. The states of A are to be
the 
ordered pairs 
together with the k states i.
We shall only define 
partially through the table
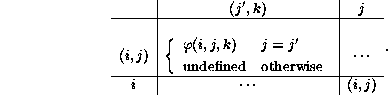
There is an enormous number of possible definitions of A, since the mixed transitions involving pairs and singlets are left undetermined. In a given case, some guidance may be available to complete the table, but for the present construction the completion is irrelevant.
To recover the operation of a from the initial configuration 
we need to see that A generates first 
and then 
Thus every second
line contains the evolution of a, but we have to be observant of how
it is positioned inasmuch as A always leaves its result in the left
cell.
In order to guarantee the substitution of a two-cell neighborhood for a
three cell neighborhood it has been necessary to augment the states by
state pairs. For a binary automaton this means that we have six states
rather than two. We defined the rule of evolution 
for just
enough arguments to ensure the recovery of the automaton a, which
means that there are really many automata capable of making the
simulation. There may be some reason for selecting the remaining
transitions in a certain way, perhaps to simplify the automaton
somehow. It also shows that one automaton may be capable of simulating
another if only one can detect the proper embedment.