Let us study some examples.
The shortest ring has one cell, which is consequently always its own neighbor. A zero must evolve into zero, while a one evolves into zero, which must repeat itself thereafter.
This result applies specifically to Rule 22, but it is equally applicable to any other rule for which uniform neighborhoods have the same transitions. General binary rules admit other possibilities, four altogether, since a field of zeroes can either be quiescent or switch over to ones. A field of ones could do the same, so either: 1) both fields are quiescent, 2) they alternate parity in a cycle of length two, 3) zero is quiescent and one vanishes in a single generation, or 4) one is quiescent but absorbs zero after the first generation.
Naturally the more states there are, the more sequences of evolution that could be followed by uniform fields; ascertaining which one should be the first order of business in analyzing any given automaton.
There are four rings of two cells: 00 evolves into 00, 01 into 01, 10
into 10, but 11 evolves into 00. Again there are many formats for the
general case to follow, the more so the more states in the automaton;
it is a matter of how many graphs can be constructed using 
nodes
with an outgoing link for each.
There are eight rings of three cells, the shortest ring for a 
automaton in which left and right neighbors can be distinct. Shorter
rings always lack certain neighborhoods, in this case, those which are
nonsymmetrical. Therefore classifying short ring evolution is useful in
establishing common features that could eventually distinguish classes
of automata.
The transitions for three cells are:
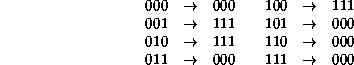
It is already evident that there are four classes with cyclic symmetry, namely {000}, {001,010,100}, {011,110,101}, and {111}, and that it would be sufficient to describe the mappings of the classes into one another.
For this purpose it is convenient to select one typical element from each class, but a class representative will not often evolve into another representative. Therefore the mapping between representatives should be supplemented with an indication of the discrepancy. A sequence of cells is naturally interpretable as a binary number, making the least number in the class a convenient representative.
Of course, there are sixteen rings containing four cells. They form six symmetry classes: {0000}, {0001, 0010, 0100, 1000}, {0011, 0110, 1100, 1001}, {0101, 1010}, {0111, 1110, 1101, 1011}, and {1111}. Individually, the transitions are
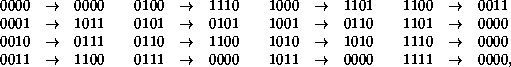
so that the economy of listing the transitions by class becomes more and more evident:
Writing down lists of transitions, either between rings or between symmetry classes, does not show the structure of the transitions to very good advantage. It is better to group them into transitive chains, in which an evolutionary sequence is shown until it repeats. Only maximal chains should be shown, which means beginning with a ring which has no ancestor if the chain has one. Sometimes there are cycles which have no ancestors outside the cycle. Since evolutionary sequences tend to converge, it may be necessary to mark some chains as continuing in another chain that has already been presented.
If we give this treatment to the thirty two chains of five elements, the result is surprisingly compact; there are eight symmetry classes, seven of which form a sequence terminating with pure zeroes, and another which evolves to zero independently (enclosing a string of classes in parentheses signifies that the string forms a cycle).
There are sixty four chains of length six, which fall into thirteen symmetry classes (the confluence of one chain with another is indicated by enclosing the junction in square brackets).
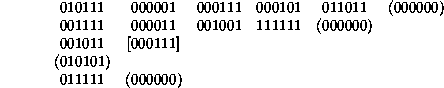
Several formal representations of sequences of this kind exist; two of them are through graphs and their connectivity matrices.