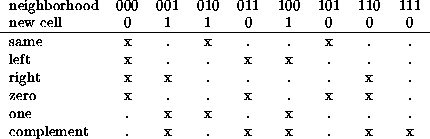
Neighborhoods in which the central cell does not change can be read off from the evolutionary rule. The complication in finding sequences which do not change lies in the overlap between neighborhoods of two successive cells. Fortunately there already exists a diagrammatic technique for dealing with overlapping sequences of symbols, which is commonly encountered in the theory of shift registers[44]. The underlying combinatorial theory goes back at least to the last century[98].
To see how this works, let us calculate the still lifes for Rule 22. The table below shows quite a bit more information than this; each transition is classified as to whether the new cell is the same as the old, as its left or right neighbor, whether it has evolved into zero or one, or the complement of its old value. In general the new cell could be tested against any Boolean function of the members of its neighborhood.
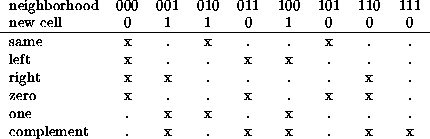
Three neighborhoods qualify for producing still lifes, namely 000, 010,
and 101. 000 can overlap only with itself in either direction, so that
it can only participate in a chain of pure zeroes. Such a chain does in
fact remain zero, so it qualifies as a still life. The other two
neighborhoods can overlap each other in alternation, leading to the
sequence 
which is also seen to be a still life.
These two alternatives exhaust the possibilities, and answer the
question ``What are the still lifes of Rule 22?''
There are three neighborhoods whose central cell evolves into one,
namely 001, 010, and 100. The first of these can only fit between the
third and the second, in that order. The second can only fit between
the first and third, and the third must follow the second and precede
the first. Thus only the sequence 
can
produce pure ones. On inspection this is reasonable---contiguous ones
necessarily force a zero, while a gap of zeroes longer than two can
never be filled with ones in a single generation.
Similar arguments can be given regarding the remaining lines in the table. However, something more concrete than such verbal arguments is required, and is afforded by the subdiagrams of a map outlining all the possible ways in which the neighborhoods defining the evolution can overlap.