Arden's lemma

If this point of view is adopted, then we have three rules of inference.

• two expressions equal to a third are equal to each other
• an expression may be substituted for an equal expression
• the solution to is

The notation stands for the continued alternative and is read ``a star.'' Any symbolic expression constructed by the aid of concatenation, alternative selection, and the star operation, is called a regular expression. Regular expressions are ideally suited to describing paths through a diagram. and conversely, any regular expression has a diagrammatic representation. Conway's monograph[25] is a concise reference for regular expressions and their properties.

If we apply these principles to the de Bruijn diagram for Rule 22 above, we find the following chain of substitutions

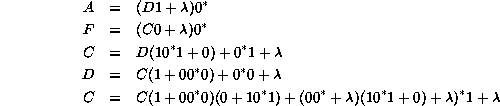
Finally we have

of which the leading term is significant and the remainder represent transients.

Although we have set up the equations for the evolution of one generation of a automaton for the special case of Rule 22, in fact the equations have the same form for all rules. Given the general evolution table

the equations are, in symbolic form,

with the general solution

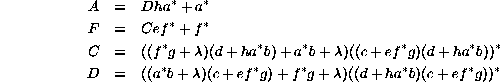
For symmetric rules we would have b= h and e = g. If 0 were a quiescent state, we would have a = 0.

For infinite or cyclic chains the interesting part of these solutions would be the starred right hand expression common to the four nodes. In essence the remainder of the expression tells how to get to the designated node from any other, while the main term tells how to keep returning to that node. For purposes of reference we could tabulate the results for all the symmetric, quiescent rules for automata. These are just Wolfram's ``legal'' rules.

 
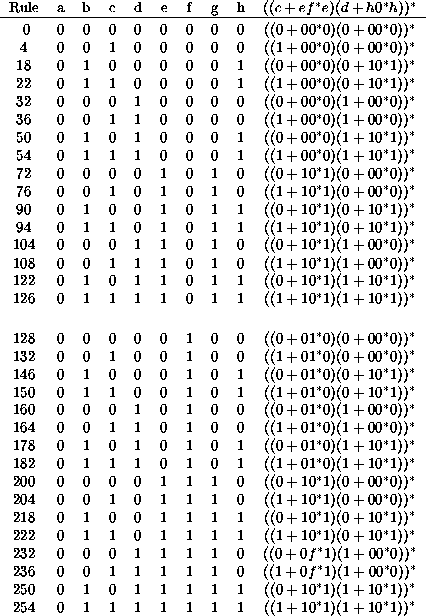
Table: Paths through the de Bruijn diagrams of Wolfram's ``legal'' Rules.