Now that we have all the derivatives for the second generation of Rule
18, it is possible to calculate its factors using the representation
that they are intersections of the derivatives. The easiest way to
calculate an intersection is to represent each intersectand via its
diagram, collect corresponding nodes into pairs, and work out the
regular expression representing the terminal nodes in this new diagram.
A terminal pair is one which is terminal for both of its components,
signified by the presence of 
's in their own diagrams.
Accordingly the exit diagram for the intersections of the left
derivatives can be gotten from a table of links, which can be written
in a compact form if certain preparations are made. Define 
then deduce the links for e and its derivatives by writing
them in canonical form, and finally display all the pairwise
intersections in a matrix.
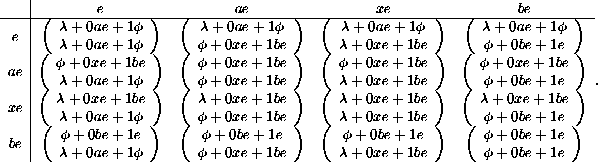
To read this array, suppose that the intersection 
is to be
calculated. Then from the row ae, column be we see from 
that the node is not terminal, that 0 leads from 
to 
and that 1 leads from 
to 
. If further
links are traced onward from these, a diagram with eight nodes is
obtained, but none of them is a terminal state. Thus this intersection
is empty, 
a conclusion which is confirmed by
observing that ae always contains an even number of 1's, while the
number of 1's in be is always odd. Since the node 
occurs in
the same diagram with 
we can also conclude that that
intersection is empty.
It is evident from the definition of xe that 
The diagram
for 
reads
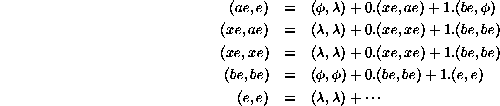
These equations can be solved by inspection to obtain
The only triple intersection not deducible from the foregoing results is
finally giving us all the possible right factors. By examining
canonical forms for the derivatives these results can be somewhat
simplified to the forms shown in parentheses. As was to be expected,
they all involve incomplete segments of the basic unit in 
All told, including the null intersection 
they are seven
in number---
ae, be, 
0ae, and 
By repeating essentially the same calculation with 
the left factors are found to be 
ef, eg,
ef0, and 
In general, the n-fold intersections can be deduced from a table of n-tuples, and in each case a diagram can be made up and solved to determine the regular expression corresponding to each intersection. The only slight doubt that might remain is whether the diagram could be reduced, due to the unsuspected equality of some of its nodes. Sometimes this is evident from inspection; as when two different nodes solve the same equation, or when the expression is fairly short with a clear interpretation. Otherwise it might be necessary to resort to testing the diagram for equivalence classes.
Having developed this theory to a fair degree of elaboration, the question naturally arises as to its applicability. For studying infinite or cyclic systems formed from symmetric rules, it does not seem likely that there will be a useful distinction between left factors and right factors; they seem more related to starting up or ending a finite expression, as the analysis which we have made for Rule 18 shows. They are also likely to be of importance for rules which admit fuses or gliders.
On the other hand, it cannot be denied that the combination of Arden's lemma and the calculus of regular expressions yields a very concise and elegant way to describe diagrams symbolically.