Block probabilities for linear chains can be defined and their
properties described by an extremely elegant matrix formulation. Binary
sequences already illustrate the principles quite clearly, as we can
see by writing the equations defining block probabilities up to length
two. Generally it is understood that 
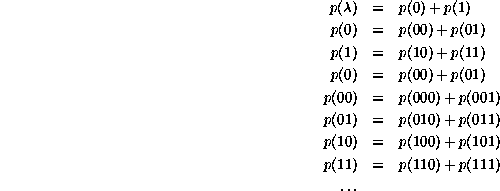
Concentrating on the last group of equations, four 2-block probabilities are written as linear combinations of eight 3-block probabilities:
.2em
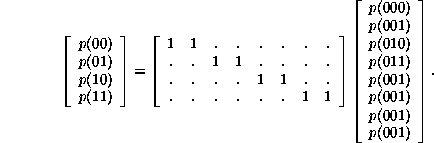
If 
is a row vector, I a unit matrix, the matrix in the
above equation can be written as a tensor product, 
However, there is another way that the same system of equations can be written, which is: .2em
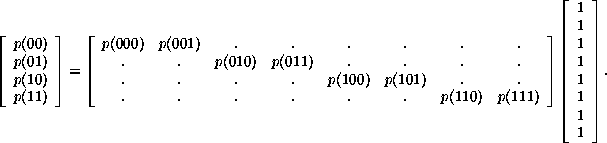
Next, we partition the rectangular matrix of probabilities into two
square matrices A and B, and partition the column of eight 1's
correspondingly into two identical columns. Then, in terms of
submatrices, the right hand side of this equation takes the form
Finally the equations relating 2-blocks to 3-blocks become .2em
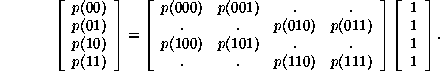
in which the matrix 
will be recognized as having the form of
a three-stage de Bruijn matrix, but with probabilities as non-zero
elements.
The interesting point is that this entire derivation can be repeated, with slight variations, for left extension rather than right extension, to obtain the 2-block probabilities as sums of 3-block probabilities. The same ``de Bruijn'' matrix will make its appearance if we write the 2-block probabilities as a row vector rather than a column vector:
.2em
In this form, the Kolmogorov consistency conditions require that the row sums of the ``de Bruijn'' matrix match the column sums. The reason that the adjective `de Bruijn' has been enclosed in quotes is that this is not quite the matrix which we intend to honor by such a description; the term is reserved for a slightly different matrix for which the consistency conditions will be met.