The generic form of a 
matrix with unit column sum is
whose eigenvalues are
whose matrix of left eigenvectors is
and whose matrix of right eigenvectors is
The eigenvalue 1, whose eigenvector has components proportional to the
off diagonal elements of the matrix, represents an equilibrium
probability. The second eigenvalue lies in the range 
with an eigenvector suitable for probability differences.
Indeed it is the factor by which the disequilibrium decreases in each
generation; if it is zero equilibrium is reached in one step, otherwise
there will be an exponential approach to equilibrium. Depending on the
sign, there may be oscillations about equilibrium, or a uniform
approach to equilibrium. However, if the second eigenvalue is as large
as one, there will either be a degeneracy by which any probability is
in equilibrium, or the probabilities for zeroes and ones will be
exchanged with each other and alternate forever after.
A doubly stochastic one-stage de Bruijn diagram would have a probability matrix
with q = 1 - p, whose eigenvalues would be 
;
being symmetric, the matrix of both left and right eigenvectors would be
The probability matrix of a two stage diagram is a little more complicated.
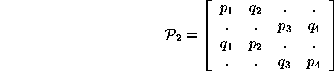
with 
and the characteristic polynomial
with two determinants defined by
The determinant of the de Bruijn matrix is the product of two smaller determinants corresponding to the evident blocks in the de Bruijn matrix; in this we have a special case of a quite general result. The p's and q's were defined as they are with the thought of equating the subscript pairs (1,2) and (3,4) to get a doubly stochastic matrix, but the best interpretation of the vanishing of the small determinants is that the biases of the probabilities in their submatrices are equal.
The constant term in the characteristic equation will be zero, giving a
single zero root, if either determinant is zero. The coefficient of
will also be zero if both are zero, producing a double zero
root. In order to get three equal roots and thus open up the
possibility of the Jordan normal form, requires some similarity between
the two submatrices in addition.