
Instead of working with formula bearing quadruples, we could have represented the links in the vector subset diagram by square matrices; most of them would be singular, but calculations involving them could be carried out entirely in terms of matrix algebra. Moreover, it would be possible to ask selective questions about ancestors by examining individual matrix elements of the product; a multiple product is already indexed by the 2r letters with which the ancestor commences and the 2r letters with which it ends.
Even more useful is to construct the connection matrix of the vector subset diagram; links to the empty set can be omitted because of the triangular form of the full matrix. For the example of Rule 126, this matrix has the form

This matrix contains four distinct non-zero submatrices
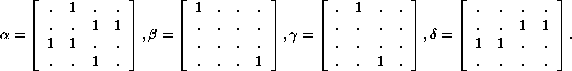
which are the matrix representations of the quadruples of the
vector subset diagram. It is convenient to regard them as hypercomplex
numbers formed from a basis consisting of the following 8 ![]() matrices
matrices
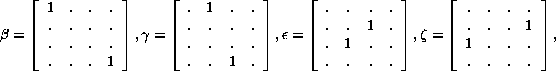
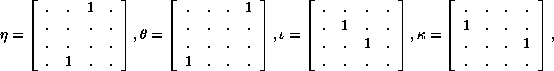
according to the definitions
![]()
These basis elements obey the multiplication table
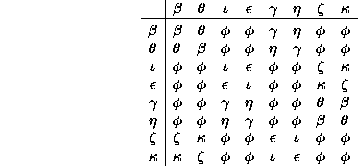
In general it is probably easier to work with the connection matrix and its powers than to deal with the algebra of hypercomplex numbers. Sometimes special properties of the algebra manifest themselves, as they do here. Every basis matrix has an even element sum, and likewise an even trace. This shows that there must always be an even number of ancestors of whatsoever open chain, and also of every ring. Thus there can be no orphan periods among the rings, in which no transients lead into the ring.
The following table shows the numbers of ancestors, of both open sequences, and rings, of three cells. To count open sequences all the elements of the final product matrix are to be summed; for rings only the trace is involved because the the ring cannot close unless the loose ends coincide.
