Date: Tue, 16 Apr 1996 23:35:55
To: ca@think.com
The background articles which we have reviewed are classics, but that does not mean that they have always been easy to understand. Partly this is due to their origins, in which sequences arose from other circumstances, such the iteration of a mapping or the solution of a differential equation. To bring understanding to sequences originating haphazardly, for all that was apparent, many kinds of periodicity were invented starting with strict periodicity, but eventually extending to recurrent, which meant that sometime, no matter how long it took, any given combination was bound to repeat, and then again, and again ... .
For that reason, Hedlund examines various backward and forward periodicities, with the intention of seeing how they are treated by the hierarchy of mappings which he distinguishes - continuous, surjective, reversible. Meanwhile, studies of subshifts take up a similar range of concepts, not always with the same vocabulary, and varying somewhat from author to author.
Were it not for concrete results, there wouldn't be much reason for theorists of cellular automata to pay too much attention to all the classification. But not only are there definite results, their counterparts in automata theory have often been overlooked, or were simply unknown. For example, much of the theory of reversible automata has lacked the benefit of the insight which symbolic dynamics could have provided.
By now, the basic theorem that cellular automata are the manifestations of continuous mappings of the shift is quite generally known and often cited. Circumstances surrounding the next result, uniform multiplicity of surjective mappings, are fairly murky, even though the result is also widely known. The difficulty arises in explaining how multiple counterimages can be guaranteed and yet only one of them is evident when the automaton is reversible.
The answer that they are indistinguishable in the limit is somewhat misleading, because unless the causes of indistinguishability are evident within a finite and calculably small distance, they will never occur. In other terms, it is all a matter of boundary conditions, and the rate at which their influence diminishes - either almost at once or never.
Still, as Richard Feynman is reputed to have once said, in giving a "physical" reason for numberical instabilities in the solution of differential equations, "You can't hide heat!" For reversible automata, the aphorism seems to be that you can hide multiple counterimages, but you can't ever get rid of them in their entirely, absolutely, completely ... .
This brings us to Welch's indices, defined for surjective mappings, and Nasu's theorem that their subset diagram contains an image of the de Bruijn diagram. It is instructive to work this out, and to observe that although it is an image, it is not always the same.
The subset diagram reveals the Garden of Eden in its entirity, but still it is not nearly as convenient for ascertaining actual counterimages. From its definition, if there is a path in the subset diagram, there are corresponding paths in the base diagram such that every point in the head subset has a path connecting it to some point in the tail subset, but not necessarily in the opposite direction. Consequently unravelling the actual path is just as much work as constructing the diagram in the first place. One solution to the problem is to define a "vector subset diargam;" another is to work with symbolic connectivity matrices, but that is another discussion for another time.
The uniform multiplicity theorem has its consequences for the subset diagram, This shows up in defining the "maximal compatible extensions" which feature in the definitions of Welch's indices, by creating a structure of ideals in the subset diagram (a fancy way of saying that the extensions of maximally compatible subsets are maximal). Paths in the base diagram, which always exist on account of surjectivity, must thread their way through the subsets in the subset diagram; they can coalesce, but never in any way creating too many paths with the same labelling. The result is a series of requirements for the intersections of the ergodic sets from the left and right subset diagrams (sets of subsets, no less) and counting theorems which Hedlund states and Nasu reiterates.
The counting theorems produce inequalities, which become equalities when shifts are bilaterally transitive. What does this mean? It can be spotted rather quickly in the pair diagram. Reversibility, or automorphism, once the subset diagram has verified surjectivity, requires that there be no loops in the subset diagram outside the diagonal. There may be transients, whose length and handedness can be related to Welch's indices, but no loops.
Mere surjectivity, or endomprphism, allows additional loops outside the
diagonal, which correspond to Hedlund's "totally (n-1)-separated shifts,"
but there is another possibility wherein the diagonal connects unilaterally
to an exterior graph. That would mean, say, that from some point onward,
counterimages which extended uniquely to the left, could diverge to the right,
even while precluded from ever rejoining. Apparently this is a combination
in which the Welch product LR attains its maximum value 
, yet the
multiplicity M is still larger than 1. So the quibbles in the theorems are
actually to be taken seriously.
Someone who would like to check this out with an actual example might examine
the 
cellular automaton CBAD1670, whose rule table is
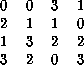
The rule has been planned to be fully quiescent in all its states; for reversible automata there is such a rule in every cluster, which need not hold for automata which are merely endomorphisms.
Examining configurations with spatial period 2, some of them lack ancestors of period 2, but rather the least period of the ancestor is 4. Examining either the pair diagram or the subset diagram shows that the phase between two such ancestors can slip exactly once, without any chance of recovering it again.
The left, or in-link, subset diagram (seen by examining the reflected rule E127B4D8) has Welch index L=1, given that the unit classes are closed under in-linkage, whilst the right, or out-link, subset diagram has Welch index R=4, given that the full set can be reached from the unit classes. Which means that it is a single-point image of the de Bruijn diagram.
Knowing that there is a fully quiescent rule in each cluster of a reversible
rule, and using Nasu's theorem about the tree rooted on each quiescent node,
the de Bruijn diagrams, or equivalently, the rule tables, for reversible
automata can almost be written down by inspection - especially when
the number of states is a prime number. Endomorphisms are more complicated -
think that only 0 is quiescent for (2,1) XOR - and the possible values of
Welch's M must be considered - but there is much less to enumerate while
searching for endomorphisms than there would be in considering all possible
rules, even after insisting on uniform multiplicity.
When the state set has composite order, even when the automaton is reversible, it is possible to split the indices between the two sides. Nasu's diagrams for Amoroso and Patt's reversible (2,3/2) automaton show the factorization 8 = 4*2; programs available nowadays permit the construction of many more examples.
The importance of the indices can be seen in another respect; anyone who has used Fredkin's scheme for constructing reversible automata will have noticed that it depends on a cartesian product from which some coordinates have been ignored. We see that this is a necessary feature of such rules; it would be interesting if a Fredkin factorization or something similar could actually be exhibited for all reversible rules.