Some surjective rules are injective, others are not. As an example of
the first kind, consider 
Rule 6, and some of the products of
ancestor matrices. Recalling the definition of 
in
Eq. 12, there is either a left or a right ancestor matrix;
choosing the right handed version, 
when
, 
otherwise. Accordingly,
0.30em
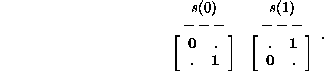
The four pair products are
0.30em
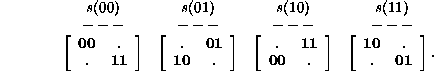
Here the detail of interest is the fact that neither the left nor the
right member of the matrix elements in 
is consistent, nor does
any such consistency arise for any of the higher order products (note
that row and column indices must also be taken into account when judging
consistency). Consequently one concludes that this rule does not have a
general purpose inverse.
Repeating the display for 
Rule 12 produces
0.30em
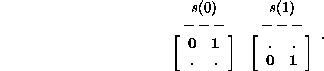
0.30em
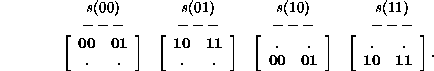
This time, there is a consistency in the left member of each ancestral pair, so that each evolved pair has a unique ancestor which can be used as the evolved state of the inverse rule, and all this quite independently of boundary conditions. Note that once consistency is found, it persists for all longer products.