Figure 24: One species moves 1 left every six generations against a background
generated by the other.
To tile the plane and thus construct an evolution, make diagonals from either tile:
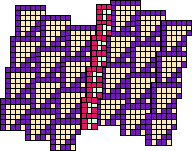
Figure 25: The second species is the glider, moving against a background
established by the first.
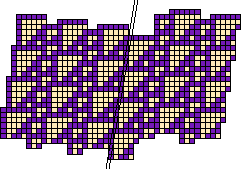
Figure 26: The first species is the glider, moving against a background
established by the second.
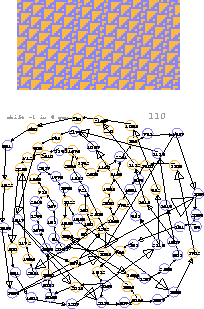
Figure 27: One species moves 1 left every six generations against a background
generated by the other.
Neither this collection nor the one with a shift 2 every five generations is as elegant as the collection which Cook and Lind have shown; nevertheless under some stretch of the imagination or other, these objects do qualify as gliders, giving both new families, and families using different arrangements of tiles than those previously seen.
It is interesting to speculate why the T3 ether fits in with so many other gliders. As we have seen, there are two different T3 packings, one of which lends itself to dislocations (or gliders) and another which does not. Also, if this is going to fit into a Class IV framework, it would be interesting to see how it jibes with mean field theory.
There the criterion was a superstable quiescent state and a superneutral other density. The ether should take the place of the superstable state, which is vaguely accomodated by what appears by such a state at 50% density. It is something to check more closely. Anyway, you do want a tenacious background. As for superneutrality, that allows a variety of forms to coexist without worrying too much about their exact density.
This is reminiscent of Eigen's Hypercycles, and is probably no more scientific than the reading of tea leaves. As to the question of why other Rules don't show gliders and all, the only readily available comparison is with Rule 22, where they are not in evidence.
This pretty much completes the survey of shifts up through generation 7. There were about as many fuses as gliders, including the property of C gliders that they can just stop at the zero configuration. What might have been expected to be an interesting doubling of the A gliders apparently isn't, although the diagram is much more complicated due to having to describe everything in terms of much longer neighborhoods. Tripling seems to give the B-bar's alongside the B's, although that would need twelve generations - unrealistic - to check and be sure, and the marginally accessible doubling in eight apparently hasn't resulted in anything which has already been observed, dilligent search presumably having been made.