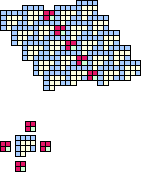
Figure 28: T1 based gliders, showing the four ways that
they may seem to be attached to the ether tile. Strings of T1's running
diagonally downwards are quite conspicuous, and a very common form of
glider.
The evolution of random configurations according to Rule 110, especially when viewed under good conditions of scale and coloring, eventually run to a proepondeance of the ether tiles, crisscrossed by trajectories which have been called gliders. The smallest, fastest, and most common of these are the A and B gliders, no doubt the reason that they were assigned the first letters of the alphabet. A gliders run right, B gliders run to the left, and both are dislocations in the etheric background caused by T1 tiles.
Speculation as to why the ether is made from T3 tiles and the gliders from T1 should probably start by realizing that the field will not be quiescent because of the left expansivity of the rule. This characteristic keeps zero density of cells in state 1 from being a stable fixed point in the return map of mean field theory; the favored density is somewhat beyond 50%.
Neither is the T1 mosaic favored; its 75% density is larger than the 63% a priori estimate taken from the rule and the mean field fixed point, and in fact higher composites of Rule 110 favor 50% as a superstable fixed point. T3 mosaics come closer to meeting the density requirements, but mesh nicely with T1's to create gliders.
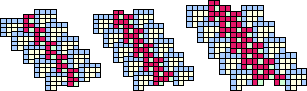
Figure 29: Thicker gliders with two, three, and four diagonals of T1's.
thicker A gliders
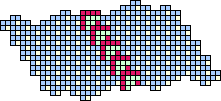
Figure 30: Turn about is fair play. T3's can appear to be gliders when displayed
against a T1 background.