![]()
Topología. Las estructuras de células y organismos vivos son organizados am-pliamente en un camino que puede ser descrito como topología, caracterizado para especificar sus posiciones como patrones de conectividad y a su vez puede obtenerse su representación matricial. La aplicación más importante de la matriz topológica consiste en su capacidad para describir caminos entre nodos conteniendo múltiples ligas de acuerdo a su evolución, por lo tanto los elementos de tales matrices son enteros y son útiles para contar el número total de caminos, pero no clasifican los caminos en diferentes categorías. Los elementos de la diagonal de la matriz cuentan los ciclos; la traza produce el número total de ciclos y cuenta cada uno de ellos una vez por cada nodo que ellos contienen.
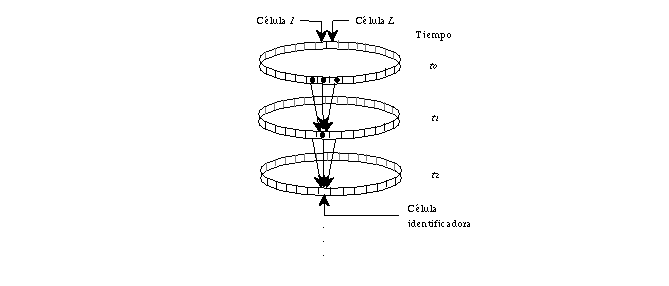
Figure 24: Anillos con condiciones de límite periódico, arreglo de
longitud L y vecindades de tamaño 3, iterando hasta un tiempo ti, (k=2,r=1).
El arreglo es ordenado como un círculo (anillo) donde la célula inicial concatena con
la célula final, tal arreglo circular tiene condiciones de límite periódico y de esta
forma establecemos la simetría dentro del autómata. La evolución del autómata puede
ser representada como una secuencia de estados globales, es decir, iteramos el estado
global inicial hasta un tiempo t determinado y cuantificamos cada uno de los
anillos hasta formar un conjunto de estos en un diagrama de evoluciones (llamados también
patrones de espacio-tiempo).
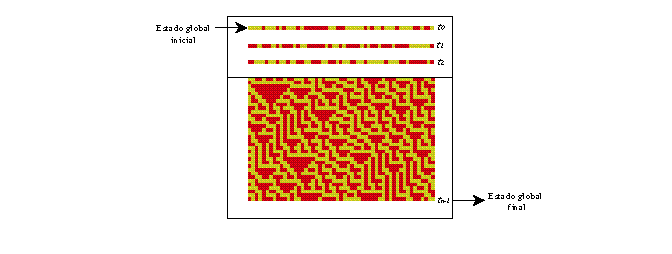
Figure 25: Diagrama de estado-tiempo, mostrando el comportamiento
(patrón) de los estados globales (anillos) de la regla 30.
Los patrones de espacio-tiempo representan las trayectorias del autómata de cualquier
estado global inicial dado. Dadas estas sencillas propiedades para cualquier autómata
podremos ver como diferentes reglas producen patrones de espacio-tiempo característicos
para una regla dada, los patrones de diferentes estados globales iniciales aleatorios son
claramente reconocidos a primera vista. Los patrones de espacio-tiempo en términos muy
amplios son construidos para mostrar el comportamiento ya sea estático, periódico,
complejo o caótico, es decir, las cuatro clases de Wolfram [11].
La clasificación de reglas para un autómata celular parecen estar hechas de acuerdo a su
fenomenología de tales patrones en el diagrama de espacio-tiempo.
El espacio-estado es el conjunto de todos los posibles estados globales en un
tiempo dado, consecuentemente en un autómata celular finito el espacio-estado es finito;
de esta manera alguna trayectoria debe encontrar eventualmente un estado global repetido
que ocurra en un tiempo dado y como el sistema es determinístico la trayectoria debe
llegar a ser localizada en una secuencia de estados repetitivos, de esta forma se llega a
formar un ciclo atractor con un período específico mayor o igual a uno.
Los estados son parte del atractor o corresponden a una transición, por lo tanto una
secuencia de estados corresponden al atractor. Si las transiciones existen deben existir
estados en los extremos llamados Jardín del Edén, esto es, una
evolución-inalcanzable para cualquier otro estado. El conjunto de todas las posibles
transiciones corresponden al atractor más el atractor mismo, esto es el basin de
atracción. Estos basins de atracción constituyen el flujo dinámico sobre el
espacio-estado dados por la función de transición del autómata.
El basin [12] de un campo de atracción de un autómata
finito es el conjunto de los basins de atracción donde todos los posibles estados y
trayectorias deben ser organizados por la función de transición del autómata. La
topología o estructura de un sólo basin de atracción puede ser descrito por un
diagrama, la gráfica de estados transición. Esto es el conjunto de gráficas
construyendo el campo específico para un comportamiento global del sistema. Algunos otros
nombres serían usados: fragmentos de estado-transición, contracción de mapas,
comportamiento topológico, red de trabajo de atracción y componentes.
Una gráfica de estado-transición liga todos los estados con un sólo basin de
atracción, de acuerdo a su evolución especifica; de esta manera debemos tener una
topológia de árboles con raices como ciclos de atracción. Los estados globales son
representados por nodos que son ligados por arcos dirigidos, cada nodo debe tener cero o
más arcos de entrada desde nodos previos en un tiempo-paso, o sea, obtener su pre-imagen;
dado que el sistema es determinístico debe existir un arco de salida a un sólo nodo (el
estado sucesor) en el siguiente tiempo-paso, los nodos que no contienen arcos de entrada
representan los estados conocidos como Jardín del Edén. El número de arcos de entrada
son referenciados como el grado de pre-imagenes sobre un nodo sucesor.
Para un conjunto de parámetros dados, el espacio-estado debe en esencia cristalizarse
dentro de un conjunto de uno o más basins de atracción, el basin del campo de atracción
es el conjunto de gráficas de estado-transición representando todos los basins dentro
del espacio-estado. Generalmente la mayoría de los nodos en los basins o un sólo basin
de atracción se localizan sobre los árboles de transiciones, fuera del ciclo atractor;
un árbol de transiciones es el conjunto de todos los caminos desde los nodos Jardín del
Edén hacia un nodo sobre el ciclo atractor (un nodo atractor); una rama del árbol de
transiciones es llamada rama transición y es el conjunto de todos los caminos desde los
nodos Jardín del Edén, que corresponden a un estado sobre el árbol de transiciones. Una
transición es un camino partícular de algún nodo arbitrario dentro del árbol que
corresponde a cualquier otro nodo, en todos los casos el nodo atractor por sí mismo es
excluido de estas definiciones.
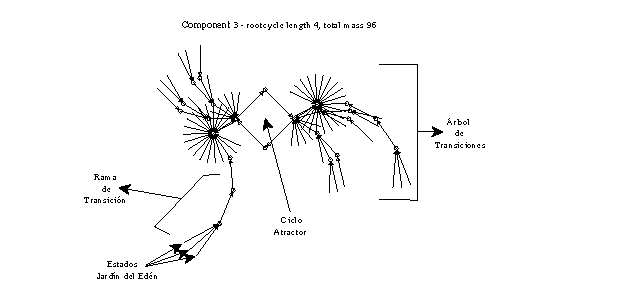
Figure 26: Gráfica de estado transición, regla 18, L = 10,
basins = 5, ciclo con período = 4, altura máxima = 5 y altura mínima = 0.
Para determinar la topología de un sólo basin de atracción conteniendo un estado
global en particular, el ciclo atractor es aislado y entonces se obtiene la topológia de
cada árbol que es especificado. Para aislar el ciclo atractor el autómata es iterado
hacia adelante en el tiempo, desde un estado global inicial seleccionado (la semilla),
hasta encontrar estados repetidos en un período dado. El número de pasos para alcanzar
la longitud encontrada es igual a las transiciones más el período del ciclo.
El período del atractor está generalmente entre 1 y algún múltiplo de L, o sea la longitud del arreglo; pero en algunos casos puede diverger exponencialmente con L para reglas con pre-imagenes limitadas. El período del atractor no puede exceder de
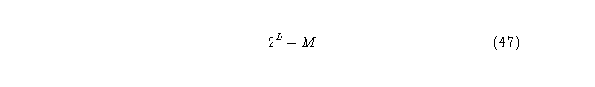
donde M es igual al número de estados dentro del espacio-estado logrados sobre
los segmentos repetidos del anillo. Si un atractor es conocido es representado como un
círculo de nodos evolucionando en sentido de las agujas del reloj. Para construir estos
árboles de transiciones es necesario tener un método que contenga el conjunto de
pre-imagenes de algún nodo, en otras palabras, para evolucionar hacia atrás en el tiempo
y de esta forma determinar todas las transiciones existentes.
La construcción de árboles y ramas de transición es simplificada a tomar ventaja del
cambio invariante, esto es, existen estados globales que se diferencian sólo por una
rotación dentro de los anillos; tal rotación equivalente debe tener pre-imagenes
equivalentes girando a una misma posición y esto debe ocupar posiciones equivalentes
dentro del mismo basin o algún otro basin equivalente. Si las pre-imagenes de sus
rotaciones equivalentes son conocidas y su extensión es el árbol de transiciones total
(o ramas de transición), no necesita ser recalculado. Si la rotación de los estados
equivalentes corresponden a basins separados, los basins deben ser equivalentes como se
ilustra a continuación:
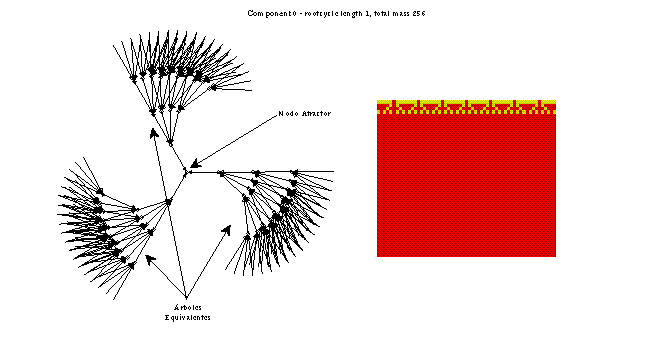
Figure 27: Un basin regla 90, L = 10, ilustrando árboles
equivalentes así como ramas equivalentes y todo el basin a su vez puede formar parte de
un conjunto de basins o componentes equivalentes (este no es el caso). Esto nos lleva a
obtener una simetría dentro del basin que mostrado en el diagrama de espacio-tiempo nos
indicaría los diferentes corrimientos de los estados globales, empezando desde un nodo
arbitrario. En este caso el patrón constante que vemos en el diagrama de espacio-tiempo
nos indica que llegó a un ciclo atractor de longitud uno.
Ahora bien, analizemos el caso en el cual el autómata a analizar sea reversible,
un autómata es reversible cuando sus configuraciones tienen uno y sólo un ancestro en el
tiempo t-i, donde la función de transición original tiene su regla inversa que
describe su comportamiento evolucionando hacia atrás en el tiempo y este comportamiento
es totalmente descifrado por la regla inversa. Dentro de los campos de atracción es
fácil determinar cuando un autómata es reversible, pues dentro de un basin o componente
no existirán arboles, ni ramas y por consecuencia la inexistencia absoluta de
configuraciones Jardín del Edén. De esta manera obtendremos únicamente ciclos de
atracción donde la masa total del árbol va a ser igual en todo momento a la longitud del
ciclo. La masa de un árbol indica el número total de estados globales que pertenecen al
componente en estudio.
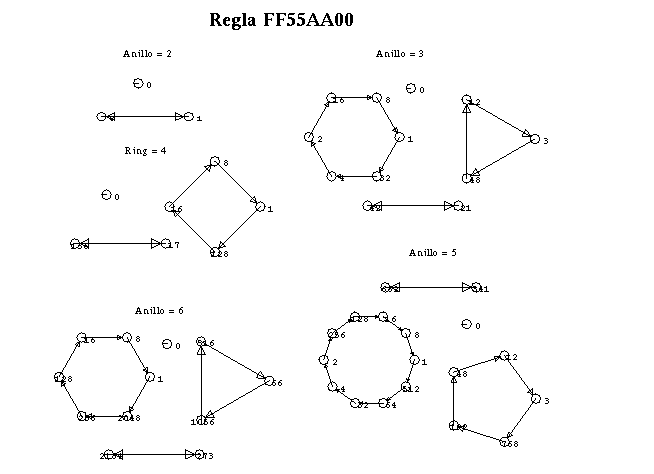
Figure 28: Autómata celular (4,h), regla FF55AA00 reversible, aquí se
muestra de manera muy clara que dado cualquier anillo de longitud L mayor o igual a
2siempre obtendremos ciclos tractores mayores igual que 1. Desde un punto de vista
general, se observa que se puede descifrar el comportamiento del autómata hacia atrás en
el tiempo a través de los componentes, esto es, uno puede seleccionar un estado global
inicial aleatorio y encontrar su pre-imagen en un tiempo-paso e iterar hacia atrás hasta
un tiempo t-i y de esta manera decifrar el comportamiento del autómata totalmente.
Los números de los nodos en el componente indican la notación equivalente en decimal de
la suma de todas las células que forman cada uno de los estados globales o anillos.
Se puede proponer en estos momentos el estudio de los componentes como una poderosa
herramienta más para describir el comportamiento de los autómatas en forma global,
además de inducir un cierto grado de reversibilidad dentro de los autómatas
sobreyectivos, es decir, que a través de una cuantificación, se pueden decifrar
configuraciones hacia atrás en el tiempo desde un estado global dado. Esto es, evitando
los múltiples ancestros; dentro de los componentes se puede apreciar como el número de
pre-imagenes en un estado global, quiere decir que para un nodo dado debemos tener a los
más una sola pre-imagen. Los componentes también pueden decifrar en un momento dado la
complejidad del autómata, mostrada en los campos de atracción.

Figure 29: En este autómata (4,h) regla FA9098C2, ciclo atractor = 6;
podemos observar la inestabilidad de los estados globales a través de todas las
transiciones existentes y es laborioso descifrar tales comportamientos.
Podemos concluir que para un autómata arbitrario, los componentes con anillos
pequeños muestran un comportamiento no tan trivial para autómatas no-reversibles, pero
si incrementamos el tamaño de los anillos, el comportamiento del componente muestra una
cierto patrón no tan evidente en configuraciones globales pequeñas y podremos de esta
forma tratar de describir el patrón del autómata. Esto es, para un autómata (2,1)
sobreyectivo, tal como la regla 30; encontramos que para sus estados globales cada vez
más grandes en un tiempo t también lo sificientemente grande; un basin con
árboles de altura considerable, consecuentemente para poder obtener el ciclo atractor
será cada vez más difícil de calcular. Sin embargo, con esto podremos darnos cuenta que
para una configuración global dada (en este caso de la regla 30), siempre obtendremos la
misma configuración cada vez que incrementemos el tamaño de los anillos sobre todo el
basin, es decir en todos los árboles.

Figure 30: Autómata (2,1), regla 30, L = 10, altura máxima = 46.
![]()