

Next: Conclusiones
Up: Cálculo del diámetro de
Previous: Aplicación del método
Para calcular el área de las burbujas, primero se considerará las de dimensión 3 y la primera que presenta un P3 o QP3 es la regla totalística 33:
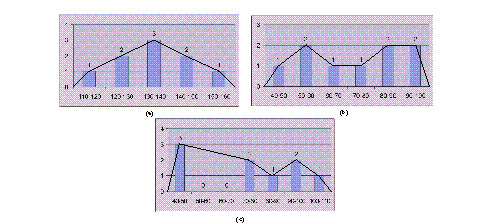
Figura 1: Los histogramas pertenecen a las tres primeras generaciones de la regla totalistíca 121 en cuatro dimensiones: (a) la primera generación, es de media densidad y tuvo un total de 1371 células vivas, (b) la segunda es de alta densidad y tiene 2185, el (c) la tercera es de baja densidad, con 624 células vivas.
si sabemos que todas las vecindades son un total de 152, obtenemos primero su polinomio de Bernstein, de aquí lo que nos interesa son el total de vecindades que se transforman en uno y son

por lo tanto todas las vecindades que se transforman a uno son 24+1=25. Si este número lo dividimos por el total de vecindades posibles 25/152= 0.16, que es una proporción de las que se transforman a uno de todas las que existen, a el resultado lo representamos en términos de porcentaje (0.16)x100% =16% dicha cantidad la convertimos en fracción y resulta 1/6, esta última fracción representa la densidad total de las burbujas que están repartidas a lo largo del autómata.
Figure 2: Regla totalística 33, vecindad de von Neumann
Por otro lado el total de miembros que componen el mosaico es 34x34=1156 esto multiplicado por la densidad total de las burbujas produce los centros de nucleación que es la distancia que existe entre las vecindades que producen burbujas 1156 x (1/6)=192.3 esta es la proporción que existe en el mosaico de dos dimensiones, pero para saber el total de burbujas que se tienen se requiere pasarlo a una dimensión, por esto se le aplica raíz cuadrada y queda (192.3)^'(1/2) = 13.87, finalmente se divide por los elementos del mosaico (en una dimension), esto para encontrar el tamaño aproximado de la burbuja 13.87/34 = 0.41.
De aquí en adelante sólo se pondrán los cálculos para los siguentes autómatas, para la regla totalística 97.
Figure 3: Regla totalística 97, vecindad de von Neumann
Para la regla totalística 121, el total de vecindades que transforman a uno son 32, entonces la densidad total de la burbuja es:
32/152 =0.21, que es el 21%, aproximadamente 7/32
El centro de nucleación:
1156*(7/32) = 252.87
Finalmente el tamaño de la burbuja es:
(252.87)^\(1/2)/34 = .47
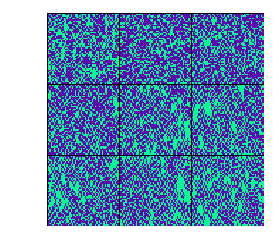
Figure 4: Regla totalística 121, vecindad de von Neumann
El total de vecindades que transforman a uno son 126 entonces la densidad total de la burbuja es: 126/152 = .82, que es el 82%, aproximadamente 5/6. El centro de nucleación: 1156*(5/6) = 915.16.
Finalmente el tamaño de la burbuja es
(915.16)^\(1/2)/34 = .89.
Para la regla totalística 123.
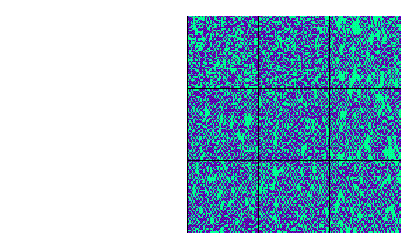
Figure 5: Regla totalística 123, vecindad de von Neumann
El total de vecindades que transforman a uno son 127 entonces la densidad total de la burbuja es: 127/152 = .83, que es el 83%, aproximadamente 5/6.
El centro de nucleación: 1156*(5/6) = 915.16
Finalmente el tamaño de la burbuja es:
915.16)^\(1/2)/34= .88
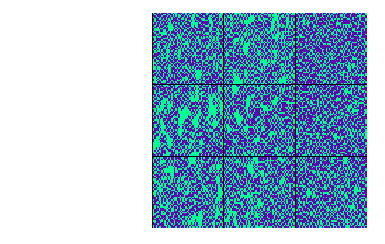
Figure 6: Regla totalística 161, vecindad de von Neumann
Para la regla totalística 161
El total de vecindades que transforman a uno son 26 entonces la densidad total de la burbuja es:
26/152 = .17, que es el 17% , aproximadamente 5/6
El centro de nucleación: 1156*(3/17) = 204
Finalmente el tamaño de la burbuja es:
(204)^\(1/2)/34 =.45
Para cuatro dimensiones los cálculos son los mismos,
sólo que ahora el tamaño del mosaico es de 50 por 50 esto hace un total de 2500 miembros en todo el mosaico y el número de vecindades totales es de 608.
Para la regla totalística 57
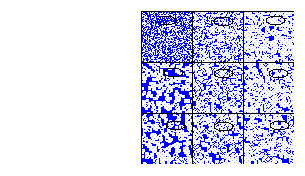
Figure 7: Regla totalística 57, vecindad de von Neumann
El total de vecindades que transforman a uno son 412 entonces la densidad total de la burbuja es:
412/608 = .67 que es el 67%, aproximadamente 2/3
El centro de nucleación:
2500*(2/3) = 1666.66
Finalmente el tamaño de la burbuja es:
(1666.66)^\(1/2)/50 =.82
Para la regla totalística 97
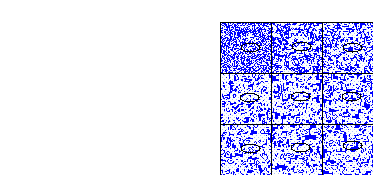
Figure 8: Regla totalística 97, vecindad de von Neumann
El total de vecindades que transforman a uno son 256 entonces la densidad total de la burbuja es:
256/608 = .42 que es el 42%, aproximadamente 17/40.
El centro de nucleación:
2500*(17/40) = 1062.5
Finalmente el tamaño de la burbuja es:
(1062.5)^\(1/2)/50 =.65
Para la regla totalística 114
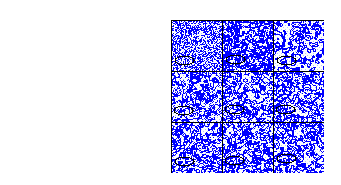
Figure 9: Regla totalística 114, vecindad de von Neumann
El total de vecindades que transforman a uno son 500 entonces la densidad total de la burbuja es:
500/608 =.82, que es el 82%, aproximadamente 5/6
El centro de nucleación
2500*(5/6)=2083.33
Finalmente el tamaño de la burbuja es:
(2083.33)^\(1/2)/50 =.91
Para la regla totalística 116
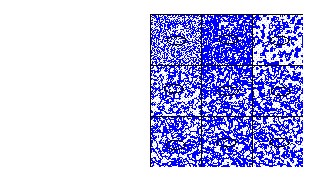
Figure 10: Regla totalística 116, vecindad de von Neumann
El total de vecindades que transforman a uno son 450 entonces la densidad total de la burbuja es:
450/608 = .74 que es el 74%, aproximadamente 23/31
El centro de nucleación:
2500*(23/31) = 1854.83
Finalmente el tamaño de la burbuja es:
(1854.83)^\(1/2)/50 =.86
Para la regla totalística 120
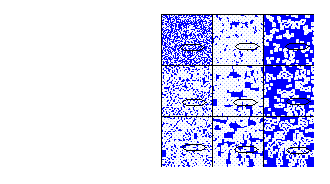
Figure 11: Regla totalística 120, vecindad de von Neumann
El total de vecindades que transforman a uno son 510 entonces la densidad total de la burbuja es:
510/608 = .83 que es el 83% , aproximadamente 5/6
El centro de nucleación:
2500*(5/6) = 2083.33
Finalmente el tamaño de la burbuja es:
(2083.33)^\(1/2)/50 =.91
Para la regla totalística 121

Figure 12: Regla totalística 121, vecindad de von Neumann
El total de vecindades que transforman a uno son 511 entonces la densidad total de la burbuja es:
511/608 = .84 que es el 84%, aproximadamente 5/6
El centro de nucleación: 2500*(5/6) = 2083.33
Finalmente el tamaño de la burbuja es:
(2083.33)^\(1/2)/50 =.91
Para la regla totalística 195
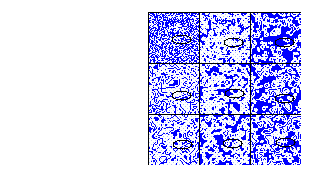
Figure 13: Regla totalística 195, vecindad de von Neumann
El total de vecindades que transforman a uno son 147 entonces la densidad total de la burbuja es:
147/608 = .24, que es el 24%, aproximadamente 1/4
El centro de nucleación
2500*(1/4) = 625
Finalmente el tamaño de la burbuja es:
(625)^\(1/2)/50 =.5
Para la regla totalística 240
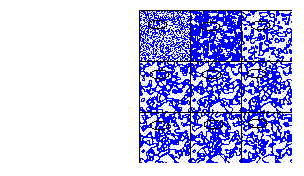
Figure 14: Regla totalística 240, vecindad de von Neumann
El total de vecindades que transforman a uno son 450 entonces la densidad total de la burbuja es:
450/608 = .74, que es el 74%, aproximadamente 23/31
El centro de nucleación
2500*(23/31) = 1854.83
Finalmente el tamaño de la burbuja es:
(1854.83)^\(1/2)/50 =.86
Para la regla totalística 289
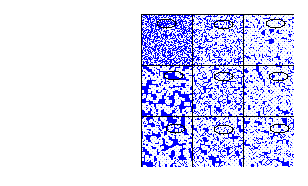
Figure 15: Regla totalística 289, vecindad de von Neumann
El total de vecindades que transforman a uno son 160 entonces la densidad total de la burbuja es: 160/608 = .26, que es el 26%, aproximadamente 1/4
El centro de nucleación
2500 *(1/4) = 625
Finalmente el tamaño de la burbuja es:
(625)^\(1/2)/50 =.5
Para la regla totalística 321
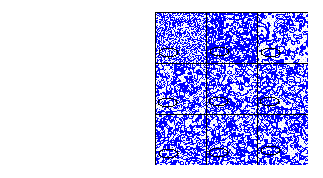
Figure 16: Regla totalística 321, vecindad de von Neumann
El total de vecindades que transforman a uno son 109 entonces la densidad total de la burbuja es:
109/608 = .18, que es el 18%, aproximadamente 7/40
El centro de nucleación
2500*(7/40) = 437.5
Finalmente el tamaño de la burbuja es:
(437.5)^\(1/2)/50 =.42
Para la regla totalística 323
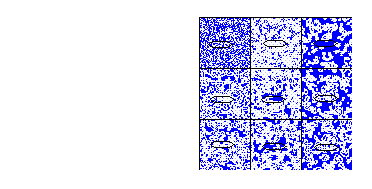
Figure 17: Regla totalística 323, vecindad de von Neumann
El total de vecindades que transforman a uno son 118 entonces la densidad total de la burbuja es:
118/608 = .19, que es el 19% , aproximadamente 1/5
El centro de nucleación
2500*(1/5) = 500
Finalmente el tamaño de la burbuja es:
(500)^\(1/2)/50 =.45
Para la regla totalística 353
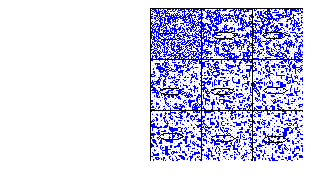
Figure 18: Regla totalística 353, vecindad de von Neumann
El total de vecindades que transforman a uno son 265 entonces la densidad total de la burbuja es:
265/608 = .43, que es el 43%, aproximadamente 17/40
El centro de nucleación
2500*(17/40) = 1062.5
Finalmente el tamaño de la burbuja es:
(1062.5)^\(1/2)/50 =.65
Para la regla totalística 368
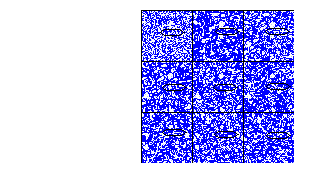
Figure 19: Regla totalística 368, vecindad de von Neumann
El total de vecindades que transforman a uno son 420 entonces la densidad total de la burbuja es:
420/608 = .7, que es el 7% , aproximadamente 22/31
El centro de nucleación
2500*(22/31) = 1774.2
Finalmente el tamaño de la burbuja es:
(1774.2)^\(1/2)/50 =.84
Para la regla totalística 385
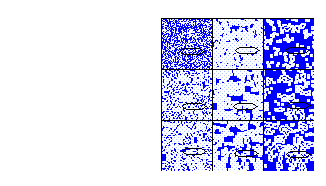
Figure 20: Regla totalística 385, vecindad de von Neumann
El total de vecindades que transforman a uno son 49 entonces la densidad total de la burbuja es:
49/608 =.08, que es el 8%, aproximadamente 1/12
El centro de nucleación
2500*(1/12) = 208.33
Finalmente el tamaño de la burbuja es:
(208.33)^\(1/2)/50 =.29
Para la regla totalística 387
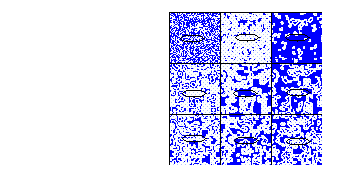
Figure 21: Regla totalística 387, vecindad de von Neumann
El total de vecindades que transforman a uno son 58 entonces la densidad total de la burbuja es:
58/608 = .09, que es el 9% , aproximadamente 1/10
El centro de nucleación
2500*(1/10) = 250
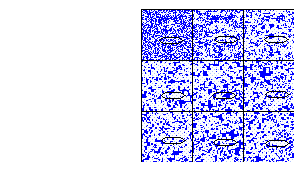
Figure 22: Regla totalística 417, vecindad de von Neumann
Finalmente el tamaño de la burbuja es:
(250)^\(1/2)/50 =.32
Para la regla totalística 417
El total de vecindades que transforman a uno son 205 entonces la densidad total de la burbuja es:
205/608 = .33, que es el 33% , aproximadamente 1/3
El centro de nucleación
2500*(1/3) = 833.33
Finalmente el tamaño de la burbuja es:
(833.33)^(1/2)/50 =.58


Next: Conclusiones
Up: Cálculo del diámetro de
Previous: Aplicación del método






















