En [20] se describe de manera muy sencilla como funciona este proceso, supongamos que tenemos los cuadros aislados de una película que representan el movimiento de una bala, si tenemos dos cuadros consecutivos de la película, una con la posición presente de la bala y otra con la posición anterior de la misma, podemos reconstruir un tercer cuadro para la posición futura y este procedimiento puede ser iterado hacia adelante o hacia atrás; justamente esta es la idea básica del método que Fredkin desarrolla.
Su método utiliza dos generaciones de células, sea 
el estado de la iésima célula en la generación t,
tenemos que la evolución de este estado está dada por 
para un ACL(2,1) donde 
representa la regla de
evolución del autómata; podemos inducir una nueva regla como 
expandiendo a dos generaciones la regla de evolución, ésto a su vez se puede invertir
como 
para la función 
podemos utilizar una
función la cual preserve la información del sistema como el or-exclusivo, el
nor-exclusivo o cualquier función invertible de dos variables, veamos dos ejemplos de
como funciona esta técnica,tomemos un ACLR(2,1) regla 240
Tomemos ahora para 
la operación or-exclusivo
Tabla: Tabla de valores para el or-exclusivo.
Observemos ahora una configuración aleatoria de células y observemos como evoluciona.
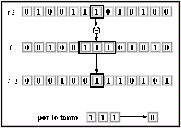
Figura: Utilizando el método de Fredkin en la evolución de una
configuración aleatoria en un ACLR(2,1) regla 240.
Tomando por ejemplo la vecindad 111 en la generación t vemos que evoluciona en 1, además que la célula central de dicha vecindad en la generación t-1 es igual con 1, por lo tanto utilizando el método de Fredkin definimos una regla secundaria en la cual la vecindad 111 evolucione en 0 para que al hacer la operación or-exclusivo con la célula central del vecindario en la generación anterior produzca la misma evolución que la regla original, repitiendo el proceso para todas las vecindades obtenemos lo siguiente.
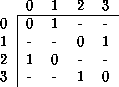
Tabla: Regla secundaria que junto con la operación or-exclusivo realizan
la misma evolución que la regla 240.
Si ahora formamos otra regla de evolución tomando en cuenta la regla secundaria y haciendo la operación or-exclusivo con la célula central del vecindario en la genaración t+1 estaremos obteniendo justamente la regla inversa a la original, repitiendo este proceso para todas las vecindades se conforma la regla 170.
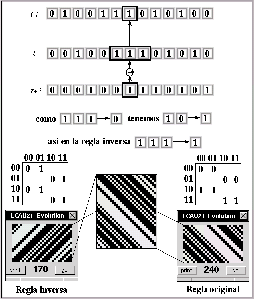
Figura: Regla 240 de un ACLR(2,1) y su regla inversa obtenida por el
método de Fredkin.
Un ejemplo para un ACLR(3,h) regla 10179, tomemos ahora la suma modulo 3 para obtener la regla secundaria, y luego aplicamos la resta modulo 3 para obtener la regla inversa a la original, en este caso la 11355.
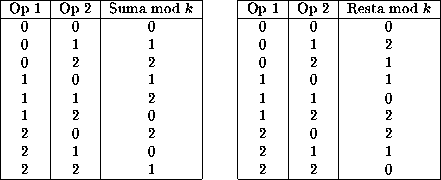
Tabla: Tabla de valores para las operaciones Suma modulo 3 y Resta modulo
3.
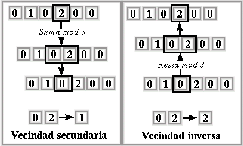
Figura: Usando el método de Fredkin con suma y resta módulo 3.
Tabla: Regla 10179 de un ACLR(3,h) y su regla inversa 11355 obtenida por
el procedimiento de Fredkin.
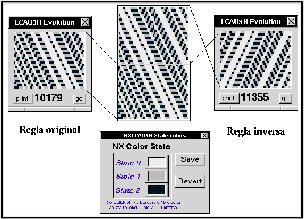
Figura: Evolución del ACLR(3,h) regla 10179 y de su regla inversa 11355.
