For the sake of continuity, this posting should be inserted in the series ``Ancestors'' after ``Reversible Automata,'' yet preceding ``Ancestors (14).'' As such it relates to both reversible evolution rules and the parameter Z (introduced by Andrew Wuensche and Mike lesser in their ``Atlas''), in the sense that there are cellular automaton rules between which restrictive relationships exist.
Actually there are many different kinds of relationships, some of them of
more interest for one application than for another. For example, given a
state set of composite order, it could be a cartesian product, supporting
two different automata acting independently. Thus, the 
(4,1) automata
include among their number 
automata whose rule of evolution is
. What an insignificant fraction!
But if they scatter well through rule space, they could be used as starting
approximations to more interesting mutants.
Cartesian products combine different rules within the same neighborhood,
but other relationships apply the same rule to different neighborhoods.
An important example is composition, which defines the evolution of an
automaton for multiple generations: consider 
via
which the single generation 
automaton becomes a 
automaton
spanning two generations. Slightly more variety is possible if two different
rules alternate between generations. This is the mechanism by which either
the identity or the complement, which are rules for 
automata, promote
themselves into rules 204 and 51 amongst (2,1) automata; they are just as
reversible in either context.
Another relationship is the one in which the rule of evolution ignores some of the cells in the neighborhood. Allowing such a possibility is not only ``mathematically correct'' (that is, general); it permits the assumption that neighborhoods are solid blocks (one consecutive interval, in one dimension). In turn, the concept of an ``edge sensitive'' rule allows distinguishing those automata whose active area does not extend out to the full limits of the neighborhood.
The appendices to Wolfram's ``Theory and Applications of Cellular Automata''
take note of both possibilities; they are implicit in Erica Jen's Table 8
(she does not identify the factors as 
automata).
Basing a theory of ancestors or of reversible rules on de Bruijn fragments supposes an awareness of their response to edge sensitivity or composition. Rule 51, whose impact on Z is described on page 41 of the Atlas, actually illustrates both concepts. First, edge sensitivity: its A and B matrices are
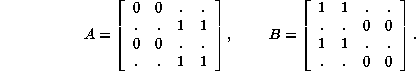
whose structure is slightly curious. Note that neither is stochastic, and tht the rule would be assigned Z=0 as a first approximation. If we now define
then
In other words A and B are each tensor products of matrices, each of which has triangular form with eigenvalues 0 and 1. The tensor products will have product eigenvalues, which will also be 0 or 1. In fact, (e, f, g, h) is part of a hypercomplex system with this fragment in its multiplication table:
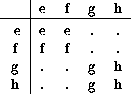
Dots indicate products (some are zero, some are new matrices) which will not occur in multiplying A and B. Although A and B do not commute, uniform multiplicity can be expected for any product of A's and B's because all the products will have a similar structure.
In fact, e and f can be recognized as a de Bruijn pair for the 
rule 
, while g and h are a de Bruijn pair for the rule
.
Although this example follows some rather clever algebra, it is really quite exceptional. The reduction of A and B to tensor products was only possible because the natural neighborhood of Rule 51 - a single cell - is detached from BOTH edges of the three-cell neighborhood in which it is immersed. However, that is the combination described in the Atlas, and it also provides a good example of a more systematic alternative.
Note that in both the A and B matrices, the bottom halves repeat the top halves as a consequence of the insensitivity of the rule to the left cell of the neighborhood. Insensitivity to the right cell is slightly more subtle, making the even columns repeat their matching odd columns, also visible in both A and B. Compare these remarks with the description of left and right templates in the Atlas, page 40 and thereafter.
With respect to the redundancy arising from ignoring the left cell, the bottom halves of A and B could be discarded without information loss. The rectangular matrices that result could be adjusted for the loss of the left cell as an index by discarding the dots, and sliding the rest of the row over to fill the hole, producing the e and f matrices, but this rearrangement gets them independently of any Kronecker product.
This sleight of hand is quite legitimate if we recall the indexing scheme for a de Bruijn matrix. If the start strings drop down from two cells to one, so should the stop strings. If we discard the first bit of the stop string, we should pick up the only part of the row containing information, which is the part whose initial bit matches the row number.
Since e and f exhibit similar structure to what we have described, but for columns rather than rows, the process can be carried a step further, to account for Rule 51's insensitivity to the right margin as well as the left. We end up with a=0 and b=1. When b=1, 0 maps into 1, and so we confirm that Rule 51 is complementation of the central cell.
If we write the transformation from A to e, B to f, in the form
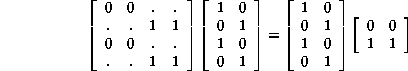
that is, AX=Xe (and also BX=Xf) (X is the rectangular matrix in the above equation), we have a formal process, which maps de Bruijn matrices of one order into those of the next lesser order. A mapping arranged in this form may seem rather mysterious, but it is standard fare in the theory of graphs. Using the formal process provides the best justification for the maneuvers described; it can also be seen underlying procedures described in the Atlas.
So at least we have a formal procedure to deflate edge-insensitive rules, which may be continued until the rule is responsive to both margins. There are also ``middle insensitive'' rules, such as Rule 90 (page 117), which evolves via the exclusive or of the two frontier cells, and only those two. Then there are the shift rules, clustered with Rule 240 (page 167), which need the n1 template. Although a shift rule can be deflated, that goes against the convention of centering the image cell with respect to its neighborhood.
But there is no problem in following the spirit of correcting Z, when
such a need arises from the rule having smaller than the nominal size of
neighborhood. What would correcting Z do to a classification scheme based
on eigenvalues of A? If v were a row eigenvector of A and 
its
eigenvalue, then 
. But then 
, while
. Hence 
, meaning that
unless vX=0, A and e have the same eigenvalues.
However, their multiplicity can (and unless X is square and nonsingular, must) differ. For the Perron eigenvalue, it is less likely that vX=0. Also, one can work back from e to A employing column eigenvectors within similar reasoning, to see what might have been lost.
Unless the largest eigenvalue were lost, there would be no penalty for deflating a neighborhood.