Here we continue an analysis of Andrew Wuensche and Mike Lesser's new book, ``The Global Dynamics of Cellular Automata.'' Addison-Wesley, 1992 (ISBN 0-201-55740-1). It is a wonderful compilation of data, and we have already commented on its complete coverage of evolution diagrams, for (2,1) automata on rings of circumference up to 15, and of selected (2,2) automata.
The first reaction of a person who intends to compile evolution diagrams
might be to make a systematic list of all the configurations, say of the
configurations on a 15-member ring; 
is only 32K, and is
still relatively manageable. An evolution graph can be created by applying
the evolution rule to each configuration, observing the configuration into
which it evolves, and noting the result in an array of links.
Many interesting statistics of the evolution diagram are available as matrix elements, vector products, or quadratic forms of this matrix. For example. the trace of its powers can be made to yield the number of loops with the corresponding length. Multiplying by a row of 1's gives a vector containing the number of out links for each node. And so on.
Many people won't even go to that much trouble; if the cycles of the automaton are all that is wanted, you just follow the evolution until the configuration repeats, and note where the loop began. By treating the configurations as binary numbers, and abandoning a search when it is found that the numbers aren't ordered satisfactorily, search time can be reduced; likewise there are sometimes advantages to generating the configurations in Gray Code order.
None of this is what Wuensche and Lesser recommend; rather, they explain a method for calculating ancestors, rather than descendants. Obviously one is not going to get the upper branches of an evolution tree by working downward, and it is impractical to compare each evolution chain with all the others to see if it has the highest nodes. The solution is to be able to work in both directions: start somewhere, go to the bottom, then work upward, identifying everything connected to the bottom. For the next tree, don't look at anything that belongs to the first one. And, in the bargain, there is no messy matrix algebra.
Calculating ancestors in a one dimensional automaton is pretty straightforward. Decide on your configuration, and start somewhere, say at the left end. By the rule table, you know what neighborhoods are going to give the first cell, so make a list of them. Now look at the second cell, whatever it is. It has its own ancestral neighborhoods, but they overlap the neighborhoods of the first cell. Discard the ones which don't match, and extend your list. But do it systematically, trying to extend the first neighborhood of the first cell in all possible ways before turning to its second neighborhood. This is a nice recursive process with a simple search strategy. In fact, it is a game of dominoes, or rather, the analysis of all possible domino games.
As extensions are made, the lists may proliferate, maintain themselves, or die out. Eventually the right end is reached; when the configuration lies on a ring, the question is whether the first cell can still be used. If so, an ancestral configuration has been found. This, amongst other things, is what we learn how to do in Chapter 3 of ``Global Dynamics.'' How many ancestors there are altogether is related to the Z-parameter, in ways that we propose to examine later on.
This is the place at which it seems that the use of some matrix theory might be useful. Once again, the de Bruijn diagram is important, and the matrix which describes its connectivity. Think of a (2,1) automaton, and ``halves'' of neighborhoods. There are four, 00, 01, 10, and 11. Let these be nodes in a graph, and let the links assert that the parts overlap to make a full neighborhood. Then 00 links to 01, and even to 00, but not to 10 nor 11. In fact, there are always two out links and two in links at each node, and we might as well label them according to the full neighborhoods. Thus link 010 joins node 01 to node 10 to form the neighborhood 010, which evolves into a 1 according to rule 22.
Make up two matrices, one for neighborhoods which evolve into 0's, one for neighborhoods which evolve into 1's. For Rule 22 we get:
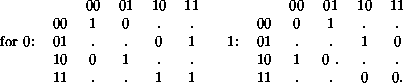
The dots in these matrices are always zeroes, indicating halves which won't join to make a neighborhood in the first place (dominoes whose spots don't match). The 0's and 1's don't mean that is the cell you get, but are boolean no's and yes's, that you will get a 0 if you are using the 0-matrix, or a 1 if you are using the 1-matrix, when that neighborhood evolves.
What makes these matrices really useful, is that when they are multiplied, they tell what kinds of chains can be formed; the rules for multiplying matrices (and the fact that zeroes and ones are being used) just end up counting the number of paths from the row node to the column node. And if a product matrix is zero, that tells that there aren't any paths at all - no ancestor, a poor little orphan, and presto! the Garden of Eden has a new resident.
Try multiplying out the matrices for 10101001. Worse yet, look at the 1-matrix for the Zero-Rule.
More commentary will follow.