Siguiente: Demostrabilidad Un nivel arriba: Irresolubilidad en la Aritmética Anterior: Irresolubilidad en la Aritmética

Aritmética de Peano

Una lógica se construye sobre un alfabeto, el cual consiste de símbolos especiales, los cuales son, usualmente, los conectivos lógicos, los cuantificadores, paréntesis y comas, de las variables y de una signatura propia, la cual consiste de constantes, funciones y predicados o relaciones. En la tabla 5.4 presentamos una signatura para la lógica de conjuntos y en las tablas 5.5 y 5.6 presentamos dos signaturas para la aritmética de Peano, sin embargo, en la presentación ulterior de la aritmética de Peano supondremos la signatura de la tabla 5.5.

 

Table 5.4: Signatura de la Teoría de Conjuntos.

 

Table: Signatura 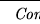$\mbox{\it AP}$ de la Aritmética de Peano.

 

Table: Signatura $\mbox{\it AP}_1$ de la Aritmética de Peano.

Si 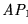${\cal L}$ es una lógica, se distinguen en ella palabras bien formadas:

Términos.

Se forman recurrentemente por las siguientes reglas:

1.

$\xi\in\mbox{\it Variables}\cup\mbox{\it Constantes}\ \Rightarrow\ \xi\in\mbox{\it T\'erminos}$.

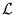2.

$f\in\mbox{\it Funciones}^n,\xi_1,\ldots,\xi_n\in\mbox{\it T\'erminos}\ \Rightarrow\ f(\xi_1,\ldots,\xi_n)\in\mbox{\it T\'erminos}$.

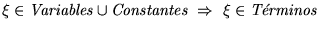Atomos.

Símbolos de relaciones ``evaluados'' en términos:

1.

$R\in\mbox{\it Relaciones}^n,\xi_1,\ldots,\xi_n\in\mbox{\it T\'erminos}\ \Rightarrow\ R(\xi_1,\ldots,\xi_n)\in\mbox{\it Atomos}$.

Fórmulas.

Se forman recurrentemente por las siguientes reglas:

1.

$\phi\in\mbox{\it Atomos}\ \Rightarrow\ \phi\in\mbox{\it F\'ormulas}.$

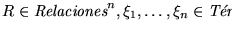
2.

$\begin{array}[t]{lcr} \phi_1,\phi_2\in\mbox{\it F\'ormulas} &\Rightarrow& \neg... ...ow \phi_2, \phi_1\leftrightarrow \phi_2\in\mbox{\it F\'ormulas}\; \end{array}$

3.

$\phi\in\mbox{\it F\'ormulas} \ \Rightarrow\ \exists x \phi(x), \forall x \phi(x)\in\mbox{\it F\'ormulas}$

Enunciados.

Fórmulas sin variables ``libres''.

Siguiente: Demostrabilidad Un nivel arriba: Irresolubilidad en la Aritmética Anterior: Irresolubilidad en la Aritmética