Siguiente: Numerabilidad de la clase Un nivel arriba: Universalidad Anterior: Universalidad

  
Codificación de programas por números

Hemos visto que los programas-while se enumeran asociándole a cada símbolo $s\in A_{\mbox{\scriptsize {\bf while }}}$, donde $A_{\mbox{\scriptsize {\bf while }}}$ es el alfabeto de programas-while , un ``dígito'' $\lceil s\rceil\in [0,a_{\mbox{\scriptsize {\bf while }}}-1],$ siendo $a_{\mbox{\scriptsize {\bf while }}}=\mbox{\rm card}(A_{\mbox{\scriptsize {\bf while }}})$. A un programa $P=p_0\cdots p_{m-1}\in A_{\mbox{\scriptsize {\bf while }}}^*$ se le asocia el ``código'' $\lceil P\rceil={\displaystyle\sum_{i=0}^{m-1}\lceil p_i\rceil a_{\mbox{\scriptsize {\bf while }}}^{m-(i+1)}}.$ Con tal codificación de programas se cumplen las relaciones siguientes:

1.

La imagen de $\lceil\cdot\rceil$ es un subconjunto propio y recursivo primitivo en $I\!\!N$.

2.

$\lceil\cdot\rceil$ es una función inyectiva.

3.

Dado el programa P se ``calcula'' procedimentalmente $n\in I\!\!N$ tal que $\lceil P\rceil=n$.

4.

Dado n en la imagen de $\lceil\cdot\rceil$, se ``calcula'' procedimentalmente el programa P tal que $\lceil P\rceil=n$.

5.

Sea $\left\{i_n\right\}_{n\geq 0}$ una enumeración recursiva primitiva de la imagen ${\cal P}$ de $\lceil\cdot\rceil$. Para cada programa-while P su índice es $n_P\in{\cal P}$ tal que $i_{n_P}=\lceil P\rceil$. Correspondientemente, escribiremos P=P_nP. La función $P\mapsto n_P$ es una biyección efectiva $\{\mbox{\rm programas-{\bf while }}\}\rightarrow{\cal P}$.

La enumeración $n\mapsto P$ es ``la'' enumeración efectiva de los programas-while . Ella cuenta a todos los programas-while y consecuentemente a todas las funciones computables. Enunciamos esto como la

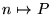
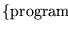
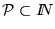
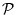
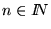
Proposición 4.1 (Numerabilidad efectiva)   La clase $\{\mbox{\rm programas-{\bf while }}\}$ se puede poner en correspondencia biunívoca con un conjunto ${\cal P}\subset I\!\!N$ de manera tal que, dado $P\in\{\mbox{\rm programas-{\bf while }}\}$ se calcula procedimentalmente el índice $n_P\in{\cal P}$ correspondiente, y dado $n\in I\!\!N$ se puede decidir procedimentalmente si acaso existe $P\in\{\mbox{\rm programas-{\bf while }}\}$ 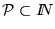tal que n=n_P y, en tal caso, se puede también construir el programa P.

Redefinimos aquí al operador $\lceil\cdot\rceil$, para escribir $n=\lceil P\rceil$, y recíprocamente, $\lfloor n\rfloor=P$, donde P y n guardan la relación expuesta en la proposición anterior. Recordamos que una función $I\!\!N^n\rightarrow I\!\!N$ se dice ser total si ella está definida para cualquier $\mbox{\bf x}\in I\!\!N^n$. En contraste con la proposición anterior, tenemos

Lema 4.1 (de la diagonal)   No existe una enumeración computable de todas las funciones computables totales.

Demostración: Supongamos que hubiera una tal enumeración, digamos que la sucesión $\left\{f_n\right\}_{n\geq 0}$ enumera de manera efectiva, vale decir, computable, a las funciones computables totales. Entonces para cualesquiera $n,m\geq 0$ el valor f_nm=f_n(m) está bien definido, y, más aún, es computable a partir de la pareja (n,m). La función $F:n\mapsto f_{nn}+1$ es pues total y computable. Por tanto debe estar en la enumeración. Luego $\exists n_F: f_{n_F}=F$, es decir $\forall m: f_{n_F}(m)=F(m).$ En particular, para m=n_F se tiene

f_nF(n_F)=F(n_F)=f+1,

lo que implica que 0=1. Esta contradicción muestra que no se puede enumerar efectivamente a todas las funciones totales.
Siguiente: Numerabilidad de la clase Un nivel arriba: Universalidad Anterior: Universalidad