


Siguiente: Field operations with the
Arriba: Multiplication in Finite Fields
Anterior: Ring multiplication
Let
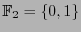 be the prime Galois field consisting of just two elements.
For most integer values
be the prime Galois field consisting of just two elements.
For most integer values 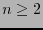 there is a minimum
there is a minimum 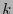 , with
, with 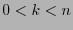 , such that the polynomial
, such that the polynomial
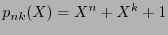 is irreducible over the field
is irreducible over the field 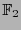 . In Table 6 we display such pairs
. In Table 6 we display such pairs 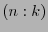 , for
, for
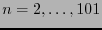 . The cases in which there is no such
. The cases in which there is no such 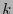 are distinguished by making
are distinguished by making 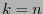 , in them any irreducible polynomial of degree
, in them any irreducible polynomial of degree 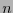 shall involve more than one intermediate powers
shall involve more than one intermediate powers 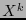 .
Whenever
.
Whenever 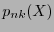 is irreducible, the Galois field
is irreducible, the Galois field
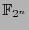 is isomorphic to the quotient
is isomorphic to the quotient
![$\mathbb{F}_2[X]/\left(p_{nk}(X)\right)$](img39.png) , and, consequently, the arithmetic in the field can be realized as the polynomial arithmetic reduced modulus
, and, consequently, the arithmetic in the field can be realized as the polynomial arithmetic reduced modulus 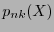 . Each element in
. Each element in
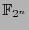 is of the form
is of the form
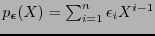 and is naturally identified with the integer
and is naturally identified with the integer
![$I_{\mbox{\scriptsize\boldmath$\epsilon$}} = \sum_{i=1}^{n} \epsilon_i 2^{i-1} \in [\![0,2^n-1]\!]$](img41.png) .
.
Table 6:
Pairs 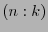 such that
such that
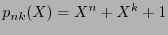 is an irreducible polynomial over the field
is an irreducible polynomial over the field 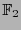 .
.
|
(2 : 1) |
(3 : 1) |
(4 : 1) |
(5 : 2) |
(6 : 1) |
(7 : 1) |
(8 : 2) |
(9 : 1) |
(10 : 3) |
(11 : 2) |
|
(12 : 2) |
(13 : 13) |
(14 : 2) |
(15 : 1) |
(16 : 4) |
(17 : 3) |
(18 : 2) |
(19 : 19) |
(20 : 3) |
(21 : 2) |
|
(22 : 1) |
(23 : 5) |
(24 : 4) |
(25 : 3) |
(26 : 26) |
(27 : 27) |
(28 : 1) |
(29 : 2) |
(30 : 1) |
(31 : 3) |
|
(32 : 8) |
(33 : 10) |
(34 : 6) |
(35 : 2) |
(36 : 4) |
(37 : 37) |
(38 : 38) |
(39 : 4) |
(40 : 6) |
(41 : 3) |
|
(42 : 4) |
(43 : 43) |
(44 : 2) |
(45 : 45) |
(46 : 1) |
(47 : 5) |
(48 : 8) |
(49 : 9) |
(50 : 6) |
(51 : 51) |
|
(52 : 3) |
(53 : 53) |
(54 : 9) |
(55 : 7) |
(56 : 2) |
(57 : 4) |
(58 : 4) |
(59 : 59) |
(60 : 1) |
(61 : 61) |
|
(62 : 6) |
(63 : 1) |
(64 : 16) |
(65 : 18) |
(66 : 3) |
(67 : 67) |
(68 : 9) |
(69 : 69) |
(70 : 4) |
(71 : 6) |
|
(72 : 8) |
(73 : 25) |
(74 : 35) |
(75 : 75) |
(76 : 21) |
(77 : 77) |
(78 : 8) |
(79 : 9) |
(80 : 12) |
(81 : 4) |
|
(82 : 6) |
(83 : 83) |
(84 : 5) |
(85 : 85) |
(86 : 21) |
(87 : 13) |
(88 : 4) |
(89 : 38) |
(90 : 27) |
(91 : 91) |
|
(92 : 2) |
(93 : 2) |
(94 : 10) |
(95 : 11) |
(96 : 16) |
(97 : 6) |
(98 : 11) |
(99 : 99) |
(100 : 12) |
(101 : 101) |
|



Siguiente: Field operations with the
Arriba: Multiplication in Finite Fields
Anterior: Ring multiplication
Guillermo M. Luna
2010-02-19
![]() be the prime Galois field consisting of just two elements.
For most integer values
be the prime Galois field consisting of just two elements.
For most integer values ![]() there is a minimum
there is a minimum ![]() , with
, with ![]() , such that the polynomial
, such that the polynomial
![]() is irreducible over the field
is irreducible over the field ![]() . In Table 6 we display such pairs
. In Table 6 we display such pairs ![]() , for
, for
![]() . The cases in which there is no such
. The cases in which there is no such ![]() are distinguished by making
are distinguished by making ![]() , in them any irreducible polynomial of degree
, in them any irreducible polynomial of degree ![]() shall involve more than one intermediate powers
shall involve more than one intermediate powers ![]() .
Whenever
.
Whenever ![]() is irreducible, the Galois field
is irreducible, the Galois field
![]() is isomorphic to the quotient
is isomorphic to the quotient
![]() , and, consequently, the arithmetic in the field can be realized as the polynomial arithmetic reduced modulus
, and, consequently, the arithmetic in the field can be realized as the polynomial arithmetic reduced modulus ![]() . Each element in
. Each element in
![]() is of the form
is of the form
![]() and is naturally identified with the integer
and is naturally identified with the integer
![]() .
.