


Siguiente: Tensores
Arriba: Geometría Diferencial y Relatividad
Anterior: Transformaciones de Lorentz
Sea
 una base de
una base de  . Naturalmente,
. Naturalmente,
 la cuarteta
la cuarteta
 se dice ser de coordenadas del punto
se dice ser de coordenadas del punto  respecto a la base
respecto a la base  (es evidente que cometemos un abuso de notación al denotar de igual manera al punto
(es evidente que cometemos un abuso de notación al denotar de igual manera al punto  y a la cuarteta
y a la cuarteta  ).
).
La base  es ortonormal respecto a la métrica de Minkowski
es ortonormal respecto a la métrica de Minkowski
![$G=\left(g_{ij}\right)_{i,j\in[\![0,3]\!]}$](img72.png) si
si  , es decir
, es decir
![$\forall i,j\in[\![0,3]\!]$](img74.png) :
:
 . Por ejemplo, la base canónica es ortonormal respecto a
. Por ejemplo, la base canónica es ortonormal respecto a 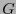 .
.
Dada otra base
 , sea
, sea
 la cuarteta de coordenadas del punto
la cuarteta de coordenadas del punto  respecto a esta nueva base. Si hubiese una transformación lineal
respecto a esta nueva base. Si hubiese una transformación lineal  tal que
tal que
 , es decir para cada
, es decir para cada  ,
,
 , entonces
, entonces
y por tanto
![$\forall j\in[\![0,3]\!]:\ {\bf e}_j = \sum_{i=0}^3\ell_{ij}{\bf f}_i.$](img84.png) Así, si
Así, si  y
y  denotan también a las matrices cuyas columnas son los correspondientes vectores básicos, se ha de tener
denotan también a las matrices cuyas columnas son los correspondientes vectores básicos, se ha de tener  . Así pues, en concordancia con la fórmula de cambio de bases:
. Así pues, en concordancia con la fórmula de cambio de bases:
![\begin{displaymath}
E=FL\ \Longleftrightarrow\ \left[\forall{\bf x}\in\mathbb{R}^4:\ {\bf u} = L{\bf x}\right]
\end{displaymath}](img87.png) |
(2.1) |
Por tanto, si  es una transformación de Lorentz, y
es una transformación de Lorentz, y  es ortonormal respecto a
es ortonormal respecto a 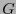 , se tiene
, se tiene
(pues  es de Lorentz). Por tanto
es de Lorentz). Por tanto  también ha de ser ortonormal.
también ha de ser ortonormal.
Recordamos que el espacio dual
 consta de todas las funcionales lineales
consta de todas las funcionales lineales
 y es en sí isomorfo a
y es en sí isomorfo a  mismo. Si
mismo. Si
 es una base de
es una base de  la base dual
la base dual
 de
de
 queda determinada por las relaciones
queda determinada por las relaciones
![\begin{displaymath}
\forall i,j\in[\![0,3]\!]:\ \langle{\bf e}^*_i\vert{\bf e}_j\rangle = \delta_{ij},
\end{displaymath}](img93.png) |
(2.2) |
y en consecuencia vale la implicación siguiente:
 |
(2.3) |
Sea  la matriz cuyas columnas son los funcionales
la matriz cuyas columnas son los funcionales  de la base dual de
de la base dual de  . Entonces, de acuerdo con (2.2),
. Entonces, de acuerdo con (2.2),
 . Por tanto, si
. Por tanto, si
 es otra base y
es otra base y  es la matriz de cambio de base según (2.1), se ha de tener
es la matriz de cambio de base según (2.1), se ha de tener
![\begin{displaymath}
E^* = F^*(L^{-1})^T\ \ \&\ \ \left[\forall{\bf y}^*\in(\mathbb{R}^4)^*:\ {\bf v} = (L^{-1})^T{\bf y}\right].
\end{displaymath}](img98.png) |
(2.4) |
donde  es la cuarteta de componentes del funcional
es la cuarteta de componentes del funcional  respecto a la base dual
respecto a la base dual  y
y  es la cuarteta de componentes de
es la cuarteta de componentes de  respecto a
respecto a  .
.
En resumen, si  es una transformación de Lorentz en el espacio-tiempo, entonces
es una transformación de Lorentz en el espacio-tiempo, entonces  es la correspondiente transformación de Lorentz en el espacio dual.
es la correspondiente transformación de Lorentz en el espacio dual.
Por ejemplo, sea
 la base canónica de
la base canónica de  . Vista como matriz,
. Vista como matriz,  coincide con la matriz identidad
coincide con la matriz identidad  de orden
de orden  . La base dual
. La base dual
 de
de
 consiste de las funciones proyecciones:
consiste de las funciones proyecciones:
Sea
 una función diferenciable. Para cada punto
una función diferenciable. Para cada punto
 la derivada
la derivada
 es un punto de
es un punto de  . De hecho
. De hecho
 . La diferencial
. La diferencial  de
de  en
en  es la transformación lineal cuya matriz es la derivada
es la transformación lineal cuya matriz es la derivada  :
:
es una funcional lineal, vale decir, es un elemento del dual
 . Así pues,
. Así pues,
 .
Sea
.
Sea  una transformación de Lorentz invertible y sea
una transformación de Lorentz invertible y sea  . La matriz
. La matriz  determina pues una base de
determina pues una base de  y el cambio de base está dado por la relación (2.1). La base dual
y el cambio de base está dado por la relación (2.1). La base dual  es también la canónica y la dual de
es también la canónica y la dual de  es
es  (según (2.4)) y así, la diferencial se representa respecto a ésta mediante la cuarteta
(según (2.4)) y así, la diferencial se representa respecto a ésta mediante la cuarteta
 .
.



Siguiente: Tensores
Arriba: Geometría Diferencial y Relatividad
Anterior: Transformaciones de Lorentz
Guillermo M. Luna
2011-01-03
![]() una base de
una base de ![]() . Naturalmente,
. Naturalmente,
![]() la cuarteta
la cuarteta
![]() se dice ser de coordenadas del punto
se dice ser de coordenadas del punto ![]() respecto a la base
respecto a la base ![]() (es evidente que cometemos un abuso de notación al denotar de igual manera al punto
(es evidente que cometemos un abuso de notación al denotar de igual manera al punto ![]() y a la cuarteta
y a la cuarteta ![]() ).
).
![]() es ortonormal respecto a la métrica de Minkowski
es ortonormal respecto a la métrica de Minkowski
![]() si
si ![]() , es decir
, es decir
![]() :
:
![]() . Por ejemplo, la base canónica es ortonormal respecto a
. Por ejemplo, la base canónica es ortonormal respecto a ![]() .
.
![]() , sea
, sea
![]() la cuarteta de coordenadas del punto
la cuarteta de coordenadas del punto ![]() respecto a esta nueva base. Si hubiese una transformación lineal
respecto a esta nueva base. Si hubiese una transformación lineal ![]() tal que
tal que
![]() , es decir para cada
, es decir para cada ![]() ,
,
![]() , entonces
, entonces

![]() consta de todas las funcionales lineales
consta de todas las funcionales lineales
![]() y es en sí isomorfo a
y es en sí isomorfo a ![]() mismo. Si
mismo. Si
![]() es una base de
es una base de ![]() la base dual
la base dual
![]() de
de
![]() queda determinada por las relaciones
queda determinada por las relaciones
![]() es una transformación de Lorentz en el espacio-tiempo, entonces
es una transformación de Lorentz en el espacio-tiempo, entonces ![]() es la correspondiente transformación de Lorentz en el espacio dual.
es la correspondiente transformación de Lorentz en el espacio dual.
![]() la base canónica de
la base canónica de ![]() . Vista como matriz,
. Vista como matriz, ![]() coincide con la matriz identidad
coincide con la matriz identidad ![]() de orden
de orden ![]() . La base dual
. La base dual
![]() de
de
![]() consiste de las funciones proyecciones:
consiste de las funciones proyecciones:
