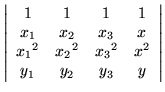Interpolation

Almost all the interpolation formulas used in numerical analysis which depend upon linear quantities such as the values, derivatives, finite differences, or the like, of data or functions can be summarized in a simple determinantal formula. For simplicity, let us consider the representation of a polynomial of second degree as a function of a single variable. We might write

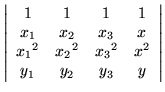$$\left\vert \begin{array}{cccc} 1 & 1 & 1 & 1 \\ x_1 & x_2 & x_3 ... ..._1}^2 & {x_2}^2 & {x_3}^2 & x^2 \\ y_1 & y_2 & y_3 & y \end{array} \right\vert$$ = 0. (1)

By inspection, it can be verified that the equation is that of a second degree polynomial, and that by well known properties of determinants, the equation is satisfied for the three pairs of points (x₁,y₁), (x₂,y₂), and (x₃,y₃).

For a higher degree polynomial it is only necessary to add more rows containing powers of the variable, and more columns with additional data points. Indeed, the method applies equally well to a function of several variables; it is only necessary to have rows for each of the basis monomials and an equal number of columns.

By using Laplace's expansion for determinants, this equation can be given a polynomial form with explicit coefficients. However, it is easy to derive a very compact form of the equation by using a little matrix algebra. Recall that the determinant of a matrix is zero if and only if there is a nonzero vector whose product with the matrix vanishes. It is convenient to partition the matrix and the corresponding vector in the following way:

$$\left[ \begin{array}{lll\vert l} 1 & 1 & 1 & 1 \\ x_1 & x_... ...}{l} 0\\ 0\\ 0\\ \hline \rule{0em}{2.5ex}0 \end{array}\right].$$

If suitable symbols are introduced for the submatrices, we have

$$\left[ \begin{array}{ll} M & X \\ Y^T & y \end{array} \right]... ...ight] = \left[ \begin{array}{l} 0 \\ 0 \end{array} \right].$$

which can be decomposed into two separate equations,

$$\begin{eqnarray*}M U + Xv & = & 0, \\ Y^T U + y v & = & 0. \end{eqnarray*}$$

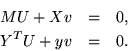
If v = 0 then U cannot be zero (we require a nonzero vector overall), and M would have to be singular, by the first equation. However M is the well known Vandermonde matrix for a polynomial basis, whose determinant cannot vanish when its data points are distinct. In the general case M is a generalization of the Vandermonde matrix, to which a similar conclusion applies. Thus it is safe to assume that M and v are both invertible.

Therefore we can rearrange the first equation to get

U = -M^-1Xv (2)

and substitute it into the second to obtain

y = Y^T M^-1 X. (3)

The components of the row vector Y^T M^-1 depend on products of two factors, the first of which is the value of the function to be represented. The second is a geometric factor, which depends only on the location of the data points and not at all on the value of the function at those points. Combined they present an explicit formula for the coefficients of the interpolating polynomial. The Vandermonde matrix has to be evaluated only once for any given set of data points.