


Next: Operaciones con cadenas
Up: Alfabetos y lenguajes
Previous: Alfabetos y lenguajes
Contents
Alfabetos, cadenas y lenguajes
Definición 2.1
Un alfabeto es un conjunto finito no vacío de símbolos y se denota como  .
.
La pertenencia de un símbolo 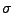 a un alfabeto
a un alfabeto  se denota como
se denota como 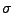
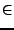
 .
.
Ejemplo: Podemos representar el alfabeto de las letras minúsculas que utiliza el idioma español, el cual contiene los 27 símbolos siguientes:
y sabemos que la letra 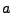 pertenece a este alfabeto, lo cual denotaremos como
pertenece a este alfabeto, lo cual denotaremos como
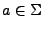 .
.
Ya sabemos que los alfabetos son conjuntos, por lo que, todas las operaciones de conjuntos se pueden aplicar a los alfabetos también. Sean
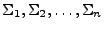 alfabetos, y ya que los alfabetos son conjuntos finitos, no vacíos, la unión de un número finito de ellos
alfabetos, y ya que los alfabetos son conjuntos finitos, no vacíos, la unión de un número finito de ellos
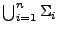 resulta en un conjunto no vacío y finito, esto es, si
resulta en un conjunto no vacío y finito, esto es, si
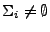 y
y
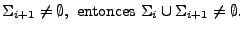
La unión de un número arbitrario finito de alfabetos resultará en un conjunto finito y no vacío, es más, si 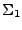 y
y 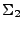 , son conjuntos no vacíos, entoces
, son conjuntos no vacíos, entoces
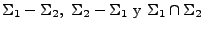 son conjuntos finitos, no vacíos, y por lo tanto serán considerados alfabetos válidos.
son conjuntos finitos, no vacíos, y por lo tanto serán considerados alfabetos válidos.
Definición 2.2
Una cadena o palabra es una secuencia finita de símbolos que pertenecen a un alfabeto y comunmente se denota con la letra 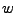 . La cadena vacía se denota como
. La cadena vacía se denota como
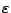 y es una secuencia vacía de símbolos tomados de cualquier alfabeto
y es una secuencia vacía de símbolos tomados de cualquier alfabeto  .
.
Sí el alfabeto es el español, algunas cadenas pueden ser 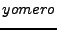 ,
, 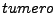 y
y 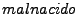 . Dada la definición anterior, cualquier palabra que contenga los símbolos del alfabeto es una cadena válida, sin importar si esta tiene o no significado alguno.
. Dada la definición anterior, cualquier palabra que contenga los símbolos del alfabeto es una cadena válida, sin importar si esta tiene o no significado alguno.
Si 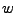 es cualquier cadena, su longitud se denota como
es cualquier cadena, su longitud se denota como 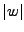 , la longitud de una cadena es el número de símbolos que contiene, por ejemplo, si tenemos la cadena
, la longitud de una cadena es el número de símbolos que contiene, por ejemplo, si tenemos la cadena
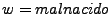 sobre el alfabeto español,
sobre el alfabeto español, 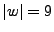 . La cadena vacía
. La cadena vacía
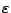 no tiene símbolos, por lo que
no tiene símbolos, por lo que
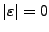
El lenguaje vacío es aquel que no contiene cadenas y no es lo mismo que el lenguaje formado por la cadena vacía
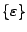 , éste lenguaje se denota de la misma manera que el conjunto vacío,
, éste lenguaje se denota de la misma manera que el conjunto vacío, 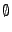 .
.
Sí se tiene una cadena 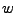 sobre un alfabeto
sobre un alfabeto  y
y 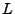 es el lenguaje compuesto por algunas de las cadenas sobre el alfabeto
es el lenguaje compuesto por algunas de las cadenas sobre el alfabeto  y
y 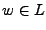 , entonces diremos que
, entonces diremos que 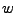 es un miembro de
es un miembro de 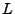 .
.
Definición 2.4
Un lenguaje universal sobre algún alfabeto  , o cerradura de
, o cerradura de  , es el lenguaje que contiene todas las cadenas que es posible formar con los símbolos de
, es el lenguaje que contiene todas las cadenas que es posible formar con los símbolos de  y se denota como
y se denota como 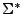 .
.
Ejemplo: Sea
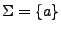 , entonces
, entonces
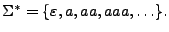
Podemos observar que para cualquier alfabeto  ,
, 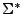 es infinito, ya que los alfabetos son conjuntos no vacíos.
es infinito, ya que los alfabetos son conjuntos no vacíos.



Next: Operaciones con cadenas
Up: Alfabetos y lenguajes
Previous: Alfabetos y lenguajes
Contents
Pablo Gerardo Padilla Beltrán
2005-10-21
![]() . La cadena vacía se denota como
. La cadena vacía se denota como
![]() y es una secuencia vacía de símbolos tomados de cualquier alfabeto
y es una secuencia vacía de símbolos tomados de cualquier alfabeto ![]() .
.
![]() es un conjunto de cadenas sobre un alfabeto
es un conjunto de cadenas sobre un alfabeto ![]() definido, éstas pueden ser cualquier cadena
definido, éstas pueden ser cualquier cadena ![]() , que cumpla con lo siguente,
, que cumpla con lo siguente, ![]() esta formada por los símbolos
esta formada por los símbolos
![]() donde
donde
![]() .
.![]() , éste lenguaje se denota de la misma manera que el conjunto vacío,
, éste lenguaje se denota de la misma manera que el conjunto vacío, ![]() .
.
![]() sobre un alfabeto
sobre un alfabeto ![]() y
y ![]() es el lenguaje compuesto por algunas de las cadenas sobre el alfabeto
es el lenguaje compuesto por algunas de las cadenas sobre el alfabeto ![]() y
y ![]() , entonces diremos que
, entonces diremos que ![]() es un miembro de
es un miembro de ![]() .
.
![]() ,
, ![]() es infinito, ya que los alfabetos son conjuntos no vacíos.
es infinito, ya que los alfabetos son conjuntos no vacíos.